Bivariate Verteilungen

Ein kurzer Überblick

Im Hintergrund ist eine Schultafel abgebildet. Davor ist ein Textfeld zu sehen: Wir wollen herausfinden, ob es bei Schüler*innen Zusammenhänge gibt zwischen der Punktezahl in einem Test, der Schlafzeit in der Nacht vor dem Test und dem Lieblingsfach.
Außerdem interessieren wir uns für mögliche Zusammenhänge zwischen Mathenote, der Sportnote und der Freizeitsportart der Schüler*innen.

Im Hintergrund ist eine Schultafel abgebildet. Davor ist ein Textfeld zu sehen: In einer Befragung wurden die Schlafdauer vor dem Mathetest, die Freizeitsportart und das Lieblingsfach der Schüler*innen erhoben.
Diesen Daten wurden die Sport- und Mathenote sowie die erziele Mathepunktzahl zugespielt.

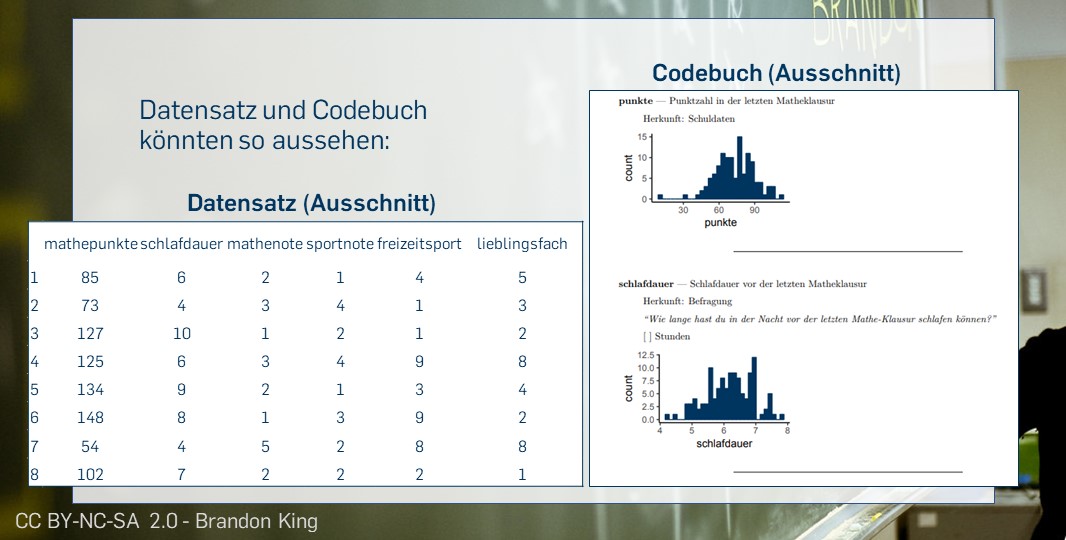
Im Hintergrund ist eine Schultafel abgebildet. Davor ist ein Textfeld zu sehen: Datensatz und Codebuch könnten so aussehen. Abgebildet sind dort ein Ausschnitt aus dem Datensatz mit acht Beobachtungen und den in Folie eins genannten interessierenden Merkmalen. Zudem ist ein Ausschnitt aus dem Codebuch zum Datensatz abgebildet, dort ist für die Variablen "punkte" und "schlafdauer" der Variablenname, eine Beschreibung der Variable, ihre Herkunft und Frage aus dem Fragebogen sowie ein Histogramm der Verteilung zu sehen.

Im Hintergrund ist eine Schultafel abgebildet. Davor ist ein Textfeld zu sehen: Je nach Art der Merkmale können wir die Zusammenhänge unterschiedlich darstellen:
1. Die Variablen Schlafdauer und Mathepunkte stellen wir als Streudiagramm dar.
Neben dem Text ist das Streudiagramm abgebildet. Die Schlafdauer in Stunden ist auf der x-Achse, die Punktezahl im Mathetest auf der y-Achse abgetragen. Die Punktewolke liegt mittig mit relativ weit verstreuten Punkten und zeigt auf dem ersten Blick keinen starken Zusammenhang zwischen den beiden Variablen auf.

Im Hintergrund ist eine Schultafel abgebildet. Davor ist ein Textfeld zu sehen: 2. Für die Darstellung der Variablen Sportart und Sporttest verwenden wir eine Kreuztabelle. Darunter ist eine Kreuztabelle abgebildet, die die Kombinationen der Ausprägungen der beiden Merkmale darstellt.

Im Hintergrund ist eine Schultafel abgebildet. Davor ist ein Textfeld zu sehen: 3. Die Merkmale Deutschnote und Mathenote stellen wir ebenfalls mit einer Kreuztabelle dar.
Unter dem Text ist eine Kreuztabelle der beiden Variablen abgebildet.

Im Hintergrund ist eine Schultafel abgebildet. Davor ist ein Textfeld zu sehen: 4. Boxplots verwenden wir z.B. für die Darstellung der Variablen Lieblingsfach und Mathepunkte.
Daneben ist das Diagramm mit den Boxplots abgebildet. Auf der x-Achse ist das Lieblingsfach und auf der y-Achse die Mathepunkte abgetragen. Für jedes Lieblingsfach ist die Verteilung der jeweiligen Mathepunkte in einem Boxplot dargestellt.

Im Hintergrund ist eine Schultafel abgebildet. Davor ist ein Textfeld zu sehen: In diesem und den nachfolgenden Artikeln wird behandelt:
- Wie anhand solcher Abbildungen Zusammenhänge zwischen den Variablen entdeckt werden können.
- Wie Zusammenhänge mithilfe von Kennzahlen berechnet und interpretiert werden können.

Hier finden Sie weitere Informationen zu den im Artikel verwendeten Beispieldaten.

Bivariate Häufigkeitsverteilungen

Wenn wir nach dem Zusammenhang zwischen zwei Merkmalen in unseren Daten fragen, interessieren wir uns — statistisch gesprochen — für die bivariate Häufigkeitsverteilung:

Welche Kombinationen von Werten zweier Merkmale treten wie häufig auf?

Was ist eine bivariate Verteilung?

Zusammenhänge in bivariaten Verteilungen

Wann würden wir in einer solchen bivariaten Verteilung einen Zusammenhang erkennen und lassen sich unterschiedliche Formen von Zusammenhängen unterscheiden?

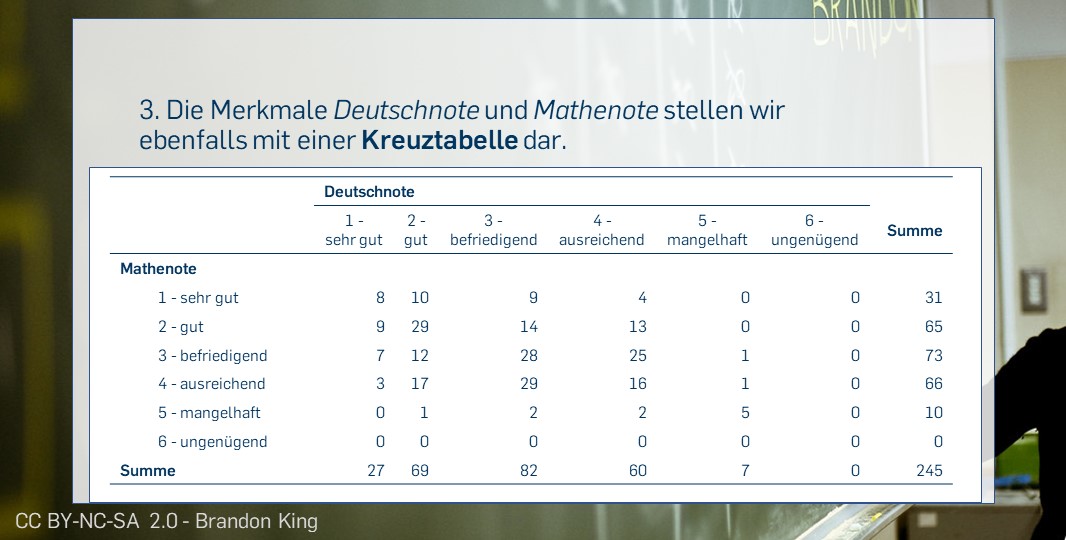
Ein Zusammenhang zwischen zwei Variablen liegt allgemein also vor, wenn die Verteilung der einen Variable (z.B. die der Mathenote) in Abhängigkeit von den Werten der anderen Variable (z.B. der Deutschnote) in irgendeiner Form unterschiedlich ausfällt. Wir sprechen von einer bedingten Verteilung: Wie bedingen die Werte der einen Variable die der anderen?

Notation für bedingte Verteilungen

Zusammenhänge nach Skalenniveau der Variablen

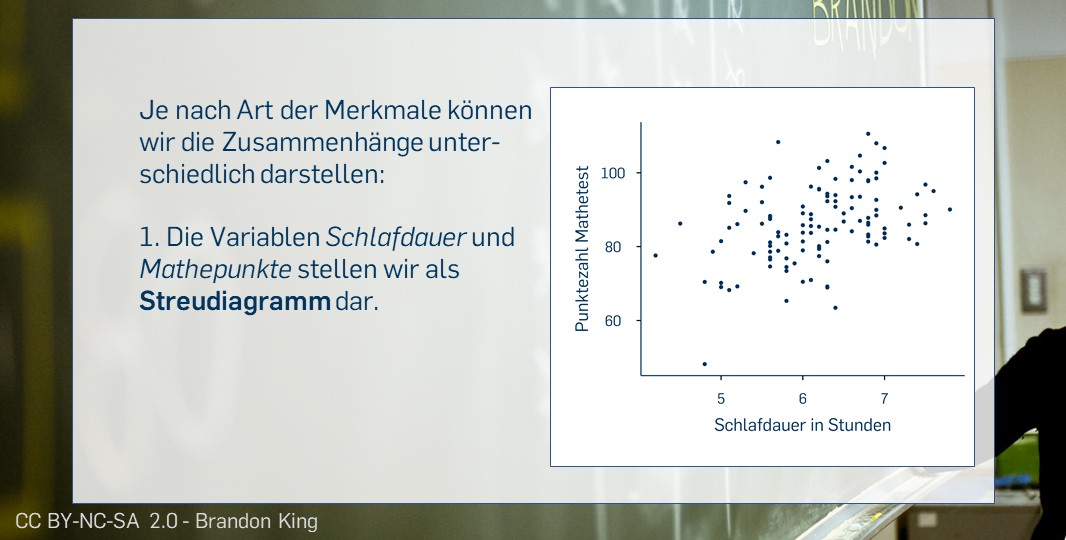
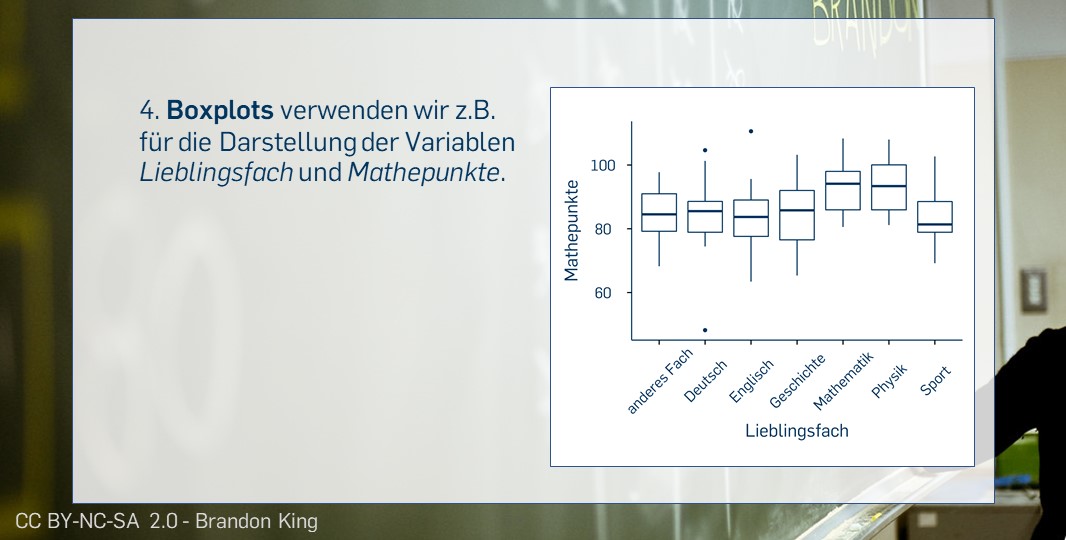
Je nach Skalenniveau (und der Anzahl der Ausprägungen) der beiden Merkmale können bivariate Verteilungen ganz unterschiedlich aussehen. Auch unsere Vorstellungen davon, wie die verschiedenen Zusammenhangsformen "aussehen", unterscheiden sich.

Stärke des Zusammenhangs und statistische Maßzahlen

Neben der Richtung (positiv/negativ) und der Form (linear/nicht linear) interessiert uns die Stärke des Zusammenhangs: Bedingen die Ausprägungen des einen Merkmal die des anderen Merkmals zu einem großen Teil oder nur in kleinerem Ausmaß? Die Abbildungen zeigen unterschiedlich starke Zusammenhänge am Beispiel der Variablen Deutschnote und Mathenote.

Statistische Zusammenhangsmaße quantifizieren die Stärke des Zusammenhangs in einer Maßzahl. Zusammenhangsmaße sind in der Regel so konstruiert, dass der Wert 0 "kein Zusammenhang" bedeutet und der Wert "1" einen perfekten Zusammenhang beschreibt. Wenn auch die Richtung eine Rolle spielt, zeigt das Vorzeichen die Richtung des Zusammenhangs an.

Für die Werte zwischen Null und Eins finden sich für viele Zusammenhangsmaße "Faustregeln", welche Wertebereiche als "schwache", " mittelstarke", "starke" Zusammenhänge usw. interpretiert werden können.

Wie bei allen Kennzahl gehen in der Darstellung mit Maßzahlen Informationen über die zu Grunde liegenden Daten verloren. Insbesondere sagen Zusammenhangsmaße nichts über die Form des Zusammenhangs aus, sondern setzen Annahmen über diese voraus. So bilden viele Maßzahlen (wie z.B. die häufig als Synonym für "Zusammenhang" verwendete "(Produkt-Moment-)Korrelation") lineare je-desto-Zusammenhänge ab. Nicht immer zeigen sie das ganze Bild:

Übersicht über bivariate Zusammenhangsmaße

Für bivariate Zusammenhänge existieren viele unterschiedliche Maßzahlen, die je nach Skalenniveau der betrachteten Variablen und Art des Zusammenhangs (linear oder nonlinear?) auszuwählen sind. Die folgende Tabelle bietet einen Überblick über verschiedene Maßzahlen für bivariate Zusammenhänge:

Zusammenhangsmaß	Skalenniveaus der beiden Variablen	Wertebereich	Aussagekraft	Beispielmerkmale
Korrelationskoeffizient \(r\)	Zwei kontinuierliche, d.h. metrische Variablen	\(-1	Stärke und Richtung eines linearen Zusammenhangs	Punktezahl Deutschtest; Schlafzeit in der Nacht davor
Cramérs \(V\)	Mindestens zwei nominale Variablen	\(0	Stärke eines Zusammenhangs	In der Freizeit ausgeübte Sportart; Sportnote
Spearmans Rangkorrelation \(\rho\) (rho)	Mindestens zwei ordinale Variablen	\(-1	Stärke und Richtung eines linearen Zusammenhangs	Deutschnote; Mathenote
\(\eta^2\) (Eta-Quadrat)	Eine metrische abhängige und eine nominale unabhängige Variable	\(0 \leq \eta^2 \leq 1\)	Stärke des Zusammenhangs	Punktezahl Mathetest; Ist Mathematik Lieblingsfach (ja/nein)

Weiterführende Artikel

Zusammenhang zwischen kategorialen Variablen

Wie kann der Zusammenhang zweier kategorialer Variablen beschrieben werden?

Kreuztabellen
Chi-Quadrat
Cramérs V

Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht-kommerziell - Weitergabe unter gleichen Bedingungen 4.0 International Lizenz.

Autor*innen dieses Artikels

Sebastian Gerhartz, Lisa Rüge

Diese Seite wurde zuletzt am 28.09.2021 aktualisiert.