Statistische Maßzahlen für Lage und zentrale Tendenz
Mit statistischen Maßzahlen für Lage und zentrale Tendenz können wir Aussagen darüber treffen, welche Werte für ein Merkmal typisch sind. Der Begriff "Lagemaße" verweist darauf, dass diese Kennzahlen anzeigen, in welchem Wertebereich der Variablen unsere Fälle "liegen". Die gängigsten Maßzahlen für die zentrale Tendenz sind der Modalwert, der Median und das arithmetische Mittel. Wie wir sehen werden wird der als "typisch" anzusehende Wert von den drei Lagemaßen ganz unterschiedlich definiert.
Die Entscheidung für eine bestimmte Maßzahl ist daher davon abhängig zu machen, welche Aussage wir genau treffen wollen. Da die Berechnung der Maßzahlen teilweise ein bestimmtes Skalenniveau der Variable voraussetzt ist die Entscheidung aber auch von der Art der zu beschreibenden Variable abhängig.
Mit Maßzahlen für die zentrale Tendenz können wir beispielsweise die folgenden Fragen beantworten:
-
Welche Punktezahl haben Schüler*innen in einem Deutschtest im Schnitt erreicht?
-
Welches ist die mittlere Anzahl an Stunden, die Schüler*innen für einen Mathetest lernen?
-
Welche ist die von Schüler*innen in der Freizeit am häufigsten ausgeübte Sportart?
Bei allen drei aufgeführten Maßzahlen handelt es sich um Mittelwerte, da sie jeweils einen mittleren, "typischen" Wert der Häufigkeitsverteilungen widerspiegeln. In einigen Fällen wird mit dem Begriff Mittelwert jedoch speziell das arithmetische Mittel benannt.
Hier finden Sie weitere Informationen zu den im Artikel verwendeten Beispieldaten.
Modalwert/Modus
Der Modalwert (häufig auch Modus genannt) ist die am häufigsten auftretende Ausprägung. Es wird also lediglich die Häufigkeit ausgezählt, mit der die einzelnen Ausprägungen auftreten und die Ausprägung benannt, die am häufigsten beobachtet wurde. Falls diese Definition auf mehrere Ausprägungen einer Verteilung zutrifft, besitzt diese entsprechend auch mehrere Modalwerte ("Modi"). Wir sprechen dann von einer "multimodalen" Verteilung.
Der Modalwert kann für Merkmale aller Skalenniveaus bestimmt werden. Für nominalskalierte Merkmale ist der Modalwert die einzige Option, etwas über "typische Werte" der Verteilung auszusagen - wenn wir nur Kategorien unterscheiden, aber nicht einmal eine Rangfolge annehmen können, sind weitere Überlegungen zu "mittleren Werten" nicht sinnvoll.
Median
Der Median beschreibt den mittleren Wert einer Variablen. Er wird daher auch "Zentralwert" genannt. Damit meinen wir die Ausprägung, die wir für den "mittleren Fall" beobachten, wenn wir alle Fälle anhand ihrer Ausprägung sortieren.
Der Median lässt sich damit anschaulich interpretieren: Die Hälfte der Fälle weist Werte auf, die höchstens dem Median entsprechen, die andere Hälfte hat Werte die mindestens so groß sind wie der Median. Der Median ist durch seine Konstruktionsweise relativ unempfindlich gegenüber "Ausreißern", also Untersuchungseinheiten mit im Vergleich sehr großen oder kleinen Ausprägungen.
Notwendig ist mindestens ein ordinales Skalenniveau der Merkmale, da die Werte sonst nicht geordnet werden könnten.
Berechnung des Medians
In diesem Abschnitt wird die Formel zur Berechnung des Medians erläutert.
Median aus einer Häufigkeitstabelle ablesen
Falls eine Häufigkeitstabelle mit relativen und kumulierten Häufigkeiten vorliegt, kann der Median einfach aus der Tabelle abgelesen werden. Bei der ersten Ausprägung, bei der die kumulierten Häufigkeiten einen Wert von \( 0{,}5 \) erreichen bzw. übersteigen, handelt es sich um den Median.
Median rechnerisch bestimmen
Zur Berechnung des Medians werden alle Werte eines Merkmals der Größe nach sortiert. So wird beispielsweise aus den folgenden Werten der Mathenote von 7 Schüler*innen {\( 2;3;1;3;2;5;2 \)} die geordnete Reihe {\( 1;2;2;2;3;3;5 \)}. Der Median ist der Wert, der in der Mitte dieser Reihe liegt. In diesem Fall ist der Median \( 2 \).
Formel für ungerade n:
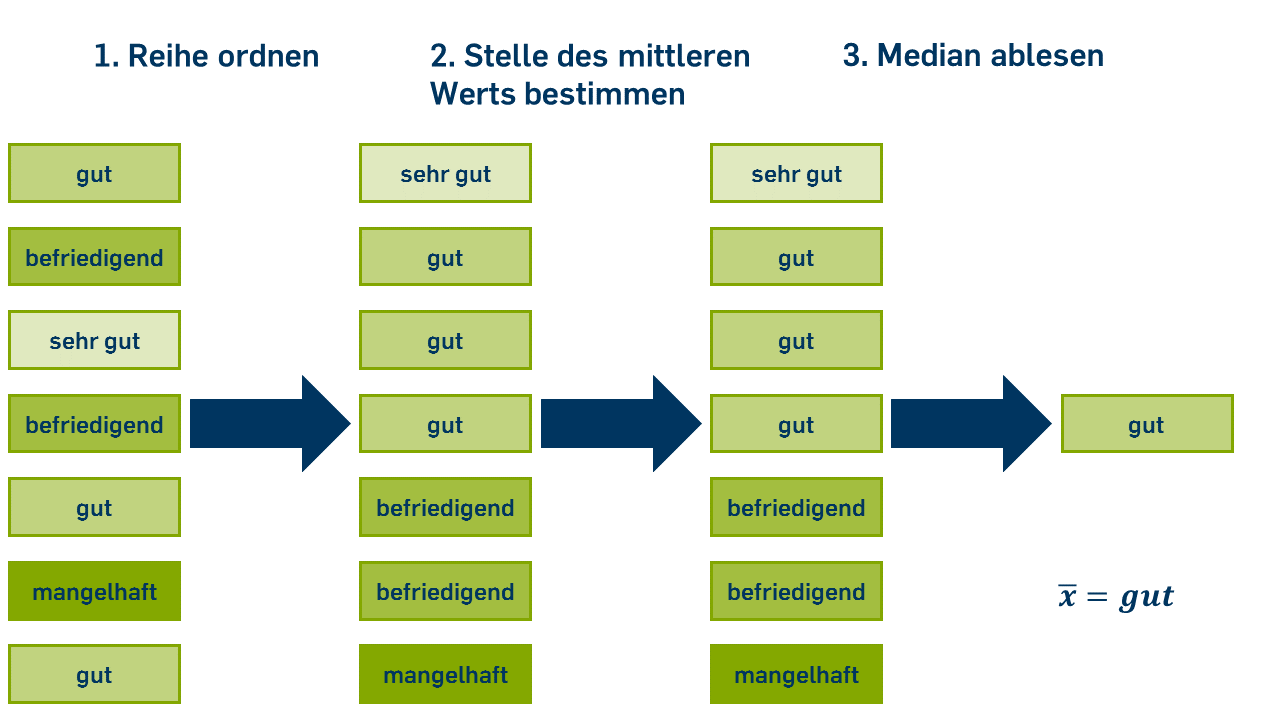
Bei einer ungeraden Anzahl von Beobachtungen gibt es einen einzelnen Wert, der in der Mitte der Verteilung liegt, nicht aber bei einer geraden Anzahl. In diesem Fall werden entweder die beiden mittleren Werte angegeben oder es wird das arithmetische Mittel der beiden mittleren Werte berechnet. Beispielsweise ist der Median einer Variable mit den Ausprägungen {\( 1;2;2;2;3;3;4;5 \)} entweder \( { 2;3 } \) oder \( 2{,}5 \).
Formel für gerade n:
oder
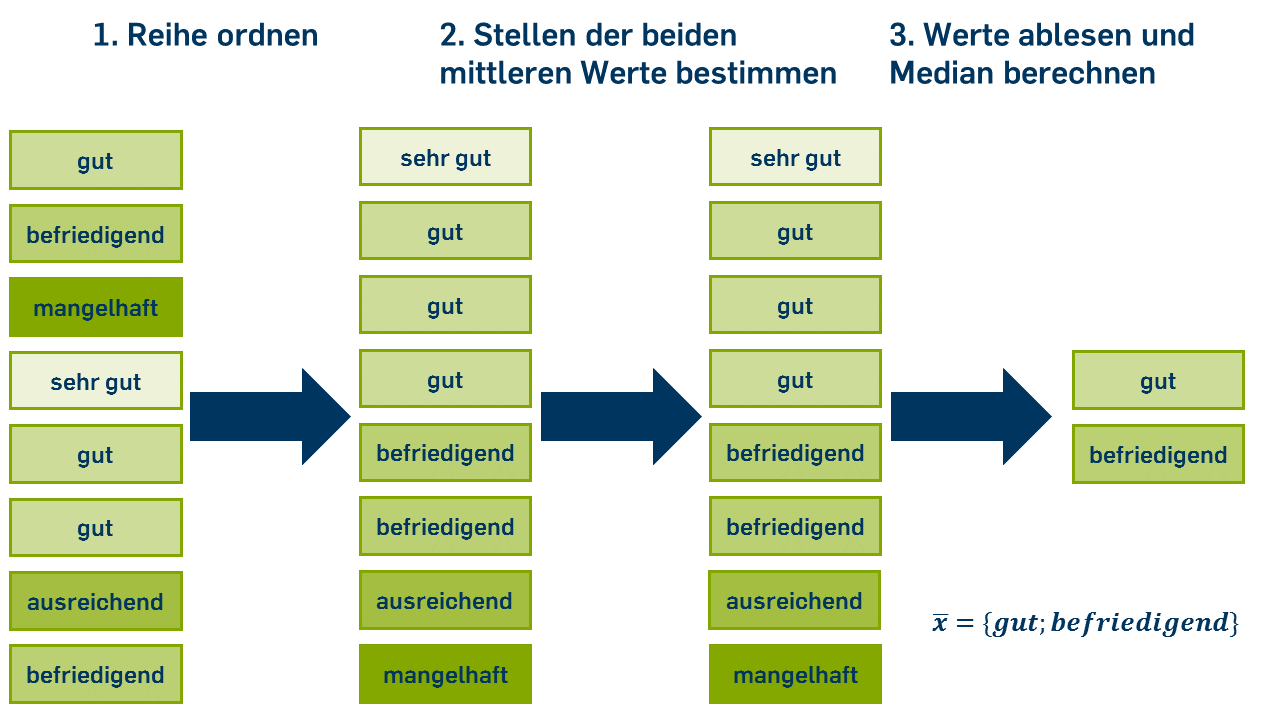
Für metrische Variablen, bei denen die Abstände der Ausprägungen interpretierbar sind, hat diese Konstruktionsweise des Medians die interessante Konsequenz, ihn realtiv "unanfällig" für Verzerrungen durch einzelne sehr große oder sehr kleine Werte zu machen (er ist nicht "ausreißersensitiv"). Sehr große Ausprägungen wirken sich nur dadurch auf den Median aus, dass die entsprechenden Fällen weit oben in der Rangfolge einsortiert werden. So könnte das "Sehr gut" im Beispiel oben genauso ein "Gut" sein, ohne dass der Wert des Medians sich ändern würde.
Quantile
In diesem Abschnitt wird gezeigt, wie sich das Konstruktionsprinzip des Medians verallgemeinern lässt und wie die Lage einer Verteilung mit Quantilen im Detail beschrieben werden kann.
Die Idee, Verteilungen in gleich große Teile (genauer: gleich häufig besetzte Abschnitte) einzuteilen, kann auch verwendet werden, um die Verteilung der Werte noch detaillierter abzubilden. Allgemein sprechen wir von Quantilen. So können wir den Median als 50%-Quantil bezeichnen. Analog dazu können wir das 30%-Quantil betrachten: 30% der Werte sind kleiner oder gleich dem 30%-Quantil, 70% sind größer oder gleich dem 30%-Quantil. Oft verwendete Quantile haben eigene Bezeichnungen, wie z.B. der Median. Weitere bekannte Quantile sind Quartile und Perzentile:
- Quartile teilen die Verteilung in vier gleich häufig besetzte Abschnitte ein. 25% der Werte sind kleiner oder gleich, 75% größer oder gleich dem ersten Quartil. Das zweite Quartil entspricht dem Median. Das dritte Quartil trennt die unteren 25% von den ober 75% einer Verteilung.
- Perzentile teilen die Verteilung in 100 gleich häufig besetzte Abschnitte ein. Für Variablen mit vielen Ausprägungen kann eine Übersicht über eine Auswahl dieser Werte einen guten Eindruck der Verteilung vermitteln. Die einzelnen Perzentil-Werte stellen (wie der Median) Lagemaße dar, in der "Gesamtschau" sehen wir aber auch die Variation der Werte ( Statistische Maßzahlen für die Streuung ).
Zum Ausprobieren: Quantile schätzen
Arithmetisches Mittel
Das arithmetische Mittel beschreibt den durchschnittlichen Wert der Variablen. Wir berechnen die Summe aller Fälle und dividieren den Wert durch die Anzahl aller Fälle. "Durchschnittlich" kann hier verstanden werden als: Die "Gesamtmenge" der beobachteten Ausprägungen wird "gleichmäßig" auf alle Fälle aufgeteilt.
Bezeichnet wird das arithmetische Mittel meist als \( \bar{x} \) (x-quer). Notwendig ist ein metrisches Skalenniveau der Merkmale.
Berechnung des arithmetischen Mittels
In diesem Abschnitt wird die Formel zur Berechnung des arithmetischen Mittels erläutert.
Das arithmetische Mittel ergibt sich aus der Summe aller Werte dividiert durch die Anzahl der Werte.
Für die folgenden Ausprägungen des Merkmals "Erreichte Punkte in einem Mathetest" \( \{85,127,125,134,54,102\} \) berechnen wir beispielsweise \( \bar{x} = \frac{85+127+125+134+54+102}{6} = \frac{627}{6} = 104{,}5 \). Die sechs Schüler*innen haben durchschnittlich \( 104{,}5 \) Punkte erreicht.
Zur Berechnung des arithmetischen Mittels wird metrisches Skalenniveau vorausgesetzt. Anders als beim Median wird hier nicht allein die Rangordnung der Werte berücksichtigt, sondern auch die Abstände zwischen den Werten - sonst dürften wir nicht addieren. Abstände lassen sich bei nominalem und ordinalem Skalenniveau nicht sinnvoll interpretieren.
Die Summe aller Abweichungen vom arithmetischen Mittel beträgt 0.
Berechnung des arithmetischen Mittels aus einer Häufigkeitstabelle
Liegt statt der Datenreihe eine Häufigkeitstabelle vor, kann das arithmetische Mittel aus den Ausprägungen \( x_1 \) bis \( x_m \) und deren Häufigkeiten \( H_1 \) bis \( H_m \) berechnet werden:
Mittelwerte im Vergleich
Aus den unterschiedlichen Berechnungsweisen folgen unterschiedliche Eigenschaften der drei Maßzahlen. Mit der folgenden interaktiven Anwendung können Sie prüfen, wie sich die Maßzahlen verändern, wenn bei Beispieldaten einzelne Fälle ausgeschlossen werden. Schließen Sie einzelne Fälle (z.B. Extremwerte) über die Schalter aus und beobachten Sie, wie sich arithmetisches Mittel, Median und Modus verändern!
Das arithmetische Mittel verändert sich deutlich in Abhängigkeit davon, ob extreme Werte in die Berechnung eingehen - wir nennen diese Eigenschaft anfällig für Ausreißer. Im Gegensatz dazu sind Median und Modus robust gegen Ausreißer.
Zusammenfassung
Praktische Umsetzung mit Statistiksoftware
Beispieldaten & R-Syntax herunterladen: [Link]
Datenbeispiel
Unser Beispieldatensatz (hypothetisches Datenbeispiel) liegt als CSV-Datei vor. Die Daten können mit der read.csv-Funktion eingelesen werden (der korrekte Pfad zum Speicherort muss angegeben werden):
dat <- read.csv("C:/... Pfad .../dat.csv")Die Funktion erzeugt ein Objekt vom Typ data.frame, dem wir links vom Zuweisungspfeil (<-) den Namen "dat" geben.
Der Datensatz enthält u.a. die Variablen punkte (erzielte Punktzahl in einem Test), schlafdauer (Schlafdauer in der Nacht vor dem Test in Std.), lernzeit (insgesamt für den Test aufgewendete Lernzeit in Std.) und lsport (Lieblingssportart). Einzelne Variablen können als Datensatzname$Variablenname angesprochen werden, z.B.:
dat$punkte
[1] 93.0 76.5 79.5 85.0 66.5 71.0 56.5 77.0 59.0 63.5 72.0 70.0 96.0 72.0 62.5 76.5 86.0 57.5
[19] 60.0 73.5 64.5 54.0 85.0 64.0 57.5 54.0 76.5 41.0 58.5 87.5 62.5 62.5 100.5 86.0 66.5 79.5
[37] 77.0 67.5 58.5 92.5 94.5 77.0 76.0 67.0 44.5 86.5 70.0 81.5 90.5 78.0 80.5 74.0 56.5 60.0
[55] 83.0 70.0 49.0 57.0 48.0 70.5 96.5 106.0 65.5 86.5 87.5 89.5 64.0 86.0 62.0 94.5 52.0 73.5
[73] 77.0 83.5 62.5 52.5 51.5 86.5 70.5 57.5 68.0 103.0 79.0 75.0 113.5 78.0 104.5 84.5 63.5 46.0
[91] 102.5 77.0 73.5 71.0 106.0 79.0 77.5 87.0 92.5 11.5 83.5 86.5 78.5 67.5 71.0 61.5 31.0 50.5
[109] 87.5 66.5 67.0 60.5 61.5 83.5 66.0 97.0 79.5 83.5 82.0 63.0Die Ausgabe zeigt die 120 beobachteten Werte der Variable punkte.
Für einen ersten Überblick über die Struktur des Datensatzes und die im Datensatz enthaltenen Variablen kann die Funktion str(dat) verwendet werden:
str(dat)liefert das folgende Ergebnis:
'data.frame': 120 obs. of 25 variables:
$ X : int 94 66 78 28 3 113 16 11 96 99 ...
$ punkte : num 93 76.5 79.5 85 66.5 71 56.5 77 59 63.5 ...
$ schlafdauer : num 6.2 5.3 5.5 7 6.5 6.4 5.7 6.8 5.4 6.8 ...
$ lernzeit : num 8.2 7 6.8 7.3 7.3 3.9 4.9 7.6 2.5 9.2 ...
$ nachhilfe : int 1 1 1 1 1 0 0 1 0 0 ...
$ zeugnis_mathe_roh : num 101.3 89.7 86.2 83.6 86.8 ...
$ zeugnis_mathe_punkte : int 13 11 10 10 10 11 9 10 9 10 ...
$ zeugnis_mathe_note : Factor w/ 4 levels "ausreichend",..: 1 2 2 2 2 2 3 2 3 2 ...
$ zeugnis_deutsch_punkte: int 8 9 10 6 10 10 9 12 5 13 ...
$ zeugnis_deutsch_note : Factor w/ 4 levels "ausreichend",..: 3 3 2 4 2 2 3 2 4 1 ...
$ lsport : Factor w/ 6 levels "Andere Sportart",..: 4 5 1 3 3 4 3 3 4 4 ...
$ sport_fb : int 0 1 0 1 1 1 1 1 1 1 ...
$ sport_bb : int 0 0 1 0 0 0 0 1 1 0 ...
$ sport_sw : int 1 1 1 1 0 0 1 1 1 1 ...
$ sport_tn : int 0 0 0 0 0 0 0 0 1 0 ...
$ sport_an : int 1 0 1 1 0 0 1 1 1 1 ...
$ sport_no : int 0 0 0 0 0 0 0 0 0 0 ...
$ sport_test : int 0 1 1 0 1 1 0 1 1 1 ...
$ kantine_zufr : int 4 4 3 5 3 2 2 1 3 2 ...
$ taschengeld : int 33 30 29 35 28 32 41 36 34 34 ...
$ lauf100 : num 14.3 13.2 13.9 14 15 14.2 14.1 14.8 15.2 13.8 ...
$ lauf1000 : num 234 229 210 222 227 ...
$ lauf5000 : num 489 465 484 486 461 ...
$ kugel : num 8.15 9.26 8.47 8.37 7.56 ...
$ lfach : Factor w/ 7 levels "anderes Fach",..: 2 2 2 2 2 2 2 2 2 2 ...Zu den einzelnen Variablen zeigt die Ausgabe deren Speicherformat (int für "integer", num für "numeric" - beides Zahlenwerte, Factor für nicht-numerische Variablen) und die jeweils ersten Werte im Datensatz.
In der Benutzeroberfläche R-Studio liefert der Data Viewer zudem einen Einblick in den Datensatz als Datentabelle. Aufgerufen wird er mit der Funktion
View(dat)So sieht ein Ausschnitt aus dem Data Viewer aus:
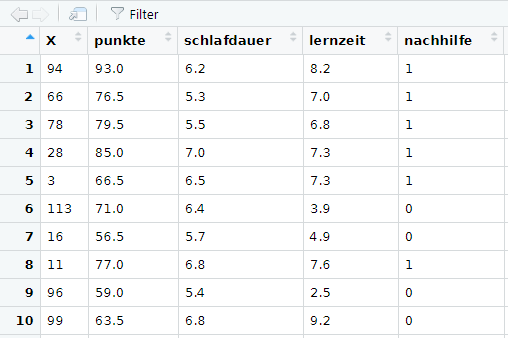
Lagemaße anhand der Funktion summary()
Einen Überblick über die wichtigsten Lagemaße bietet die Funktion summary(). Die Funktion ist generisch, d.h. sie passt ihre Berechnungen der Art der Informationen (technisch: den Objekttypen) an, die sie erhält. Verwenden wir summary() z.B. auf die numerische Variable punkte, erhalten wir das arithmetische Mittel (Mean), den Median (Median) und das erste und das dritte Quartil (1st Qu. und 3rd Qu.) sowie den kleinsten und den größten Wert der Verteilung (Min. und Max.):
summary(dat$punkte)
Min. 1st Qu. Median Mean 3rd Qu. Max.
11.50 62.50 73.50 73.23 84.62 113.50 Für eine kategoriale Variable (vom Objekttyp Factor) erhalten wir mit der Funktion summary() anstelle einer Tabelle mit deskriptiven Statistiken die Häufigkeitstabelle der Verteilung. Für die Variable lsport:
Eine alternative Möglichkeit bietet das Paket "DescTools". Wir laden das Paket mit der Funktion library(DescTools). Falls das Paket nicht installiert ist, müssen wir dies einmalig nachholen:
install.packages("DescTools") # Installation nur einmalig notwendig
library(DescTools)Die Funktion Desc gibt die zentralen Statistiken direkt aus und stellt die Verteilung grafisch dar.
Desc(dat$punkte)
Desc(dat$lsport)Wenn wir an einzelnen Maßzahlen interessiert sind, können wir alle Lagemaße auch einzeln ermitteln:
Modalwert
Der Modalwertmuss wie oben gezeigt aus einer Häufigkeitstabelle abgelesen werden. Die von der summary()-Funktion für Factor-Variablen ausgegebene Tabelle erhalten wir auch mit table(). Auf die Variable lsport (Lieblingssport) angewendet
table(dat$lsport)erhalten wir das Ergebnis
Andere Sportart Basketball Fußball
14 18 34
Keine Sportart Schwimmen Tennis
32 16 6 Fußball kommt mit 34 Fällen am häufigsten vor. Die am häufigsten genannte Lieblingssportart ist Fußball.
Die Funktion typical_value() aus dem Paket "sjmisc" kann verwendet werden, um den Modus direkt zu berechnen. Das Paket muss dazu ggf. installiert und mit library() aktiviert werden. Als Option wird fun = "mode" angegeben, um den Modus zu erhalten. Hinweis: Die Funktion gibt auch für multimodale Verteilungen nur einen Modus aus. Im Zweifel muss in der Häufigkeitstabelle geprüft werden, ob mehrere Modi vorliegen.
install.packages("sjmisc") # Paket installieren
library(sjmisc) # Paket aktivieren
typical_value(dat$lsport, fun = "mode")
. [1] "Fußball"Median
Mit der Funktion median() lässt sich der Median eines Merkmals berechnen. Für das Merkmal lernzeit verwenden wir:
median(dat$lernzeit)und erhalten als Ergebnis einen Median von 6,9. Die Hälfte der Schüler*innen hat 6,9 oder weniger Stunden für den Test gelernt.
Quantile berechnen wir mit der Funktion quantile(). Mit der Option probs geben wir an, für welchen Anteil wir den Quantilwert berechnen wollen. Für das 1%-Quantil schreiben wir 0.01, für das 12%-Quantil 0.12, usw.
Wir möchten das 25%-Quantil (also das erste Quartil) sowie das 75%-Quantil (also das dritte Quartil) der Variable lernzeit bestimmen und nutzen die folgenden Befehle:
quantile(dat$lernzeit, probs=0.25)
quantile(dat$lernzeit, probs=0.75)Es können auch Quantile für mehrere Anteilwerte gleichzeitig berechnet werden:
quantile(dat$lernzeit, probs=c(0.25, 0.75))Das erste Quartil liegt bei 5,2 und das dritte Quartil liegt bei 8,1.
Ohne Angabe von Anteilswerten
quantile(dat$lernzeit)erhalten wir standardmäßig alle drei Quartile sowie das 0%- und das 100%-Quantil:
0% 25% 50% 75% 100%
0.700 5.225 6.900 8.100 12.200 2.200 Wir benutzen die Funktion mean() für die Berechnung des arithmetischen Mittels. Das arithmetische Mittel des der Variable punkte erhalten wir mit
mean(dat$punkte)
. [1] 73.23333Das arithmetische Mittel der Punktezahl beträgt 73,2. Durchschnittlich wurden in dem Test also 73 Punkte erreicht.
Wichtige Befehlsoptionen
na.rm = TRUE bei fehlenden Werten
Liegen bei einer Variable im Datensatz nicht für alle Beobachtungsfälle Daten vor, führen diese fehlenden Werte (in R als NA gekennzeichnet) bei der Berechnung von Median und arithmetischem Mittel zu dem Ergebnis
. [1] NA
Um die fehlenden Werte bei der Berechnung auszuschließen, muss explizit die Befehlsoption na.rm = TRUE angegeben werden:
mean(dat$punkte, na.rm = TRUE)
median(dat$punkte, na.rm = TRUE)Hier entsteht ein Abschnitt zu Analyse von Lagemaßen in Stata.
Bei dringenden Fällen können Sie einen Termin zur Beratung vereinbaren.
Beispieldaten & SPSS-Syntax herunterladen: spss_lage.zip
Datenbeispiel
Arithmetisches Mittel, Median und Modalwert
Statt durch Klicken durch das Menü können wir uns die Lagemaße über die Syntax ausgeben lassen. Dazu verwenden wir den folgenden Code:
FREQUENCIES VARIABLES=punkte schlafdauer lsport
/STATISTICS=MEAN MEDIAN MODE.Wir verwenden den Befehl FREQUENCIES und geben nach VARIABLES= nacheinander alle gewünschten Variablen mit Leerzeichen getrennt an. Das Ergebnis wäre je eine Häufigkeitstabelle pro Variable. Um zusätzlich Lagemaße zu erhalten, geben wir den Unterbefehl /STATISTICS= ein mit den Optionen MEAN für das arithmetische Mittel, MEDIAN für den Median und MODE für den Modalwert. Mit dem Punkt schließen wir den Befehl ab.
Statt mit FREQUENCIES (im Menü: Analysieren -> Deskriptive Statistiken -> Häufigkeiten) können wir uns Maßzahlen alternativ mit DESCRIPTIVES berechnen. Dies kann bei metrischen Variablen mit großem Merkmalsraum von Vorteil sein, da keine Häufigkeitstabellen ausgegeben werden und über die Syntax schnell die gewünschten Maßzahlen angegeben werden können. Median und Modus können hierbei allerdings nicht ausgewählt werden. Wir verwenden entweder den Code
DESCRIPTIVES VARIABLES=punkte
/STATISTICS=MEAN.oder Klicken durch das Menü: Analysieren -> Deskriptive Statistiken -> Deskriptive Statistik -> Variablen auswählen -> Optionen -> Mittelwert -> weiter -> OK.