Tabellarische und grafische Darstellung
Tabellen und Diagramme (Grafiken, Plots, Darstellungen ...) geben uns einen Überblick über die Verteilung einer Variable — also, welche unterschiedlichen Werte eine Variable in wie vielen Fällen annimmt.
Eine direkte Betrachtung der Rohdaten in der Datenmatrix ermöglicht einen solchen Überblick in der Regel nicht. Mit Kennzahlen zu Lage und Streuung können wir die wichtigsten Aspekte der Verteilung einer Variablen erfassen, verlieren aber immer auch Informationen. Tabellarische oder visuelle Darstellungen sind deshalb in jeder Datenanalyse von Bedeutung.
In deskriptiven oder explorativen Studien kann die detaillierte Darstellung der Verteilung der Variablen ein Hauptziel der Datenanalyse sein. Für weiterführende (bi- oder multivariaten) Analysen können bestimmte Eigenschaften von Verteilungen die Anwendung einzelner Methoden einschränken bzw. erst ermöglichen.
Geeignete Darstellungsformen
Nicht jede Darstellungsform ist für alle Variablen und Verwendungszwecke gleich gut geeignet. Die folgenden Punkte sind zu berücksichtigen:
- Welches Skalenniveau hat die darzustellende Variable?
- Wie viele Ausprägungen hat die Variable?
- Wie detailliert soll die Darstellung sein? Soll jeder einzelne Datenpunkt ablesbar sein oder sind Zusammenfassungen für einen besseren Überblick erwünscht?
- Welche (Statistik-)Kenntnisse bringen die Leser*innen/Zuhörer*innen mit?
- Inbesondere bei grafischen Darstellungen: Wie groß ist die Abbildung, ist sie farbig oder schwarz-weiß?
Beispieldaten
Hier finden Sie Informationen zu den im Artikel verwendeten Beispieldaten.
Tabellen
Merkmale mit wenigen Ausprägung
Tabellen lassen sich für Merkmale jeden Skalenniveaus erstellen. Für jede Ausprägung des dargestellten Merkmals wird die beobachtete Häufigkeit aufgelistet. Oft werden neben absoluten Häufigkeiten auch Prozentwerte oder relative Häufigkeiten (bezogen auf die Anzahl aller Fälle) angegeben.
Wenn eine Rangordnung der Merkmale vorliegt (also ab ordinalskalierten Merkmalen), können zusätzlich auch kumulierte Anteile eingetragen werden, die für jede Ausprägung angeben, welcher Anteil der Fälle diese Ausprägung oder eine kleinere annimmt.
Merkmale mit (zu) vielen Ausprägungen
Wenn ein Merkmal sehr viele Ausprägungen aufweist, werden tabellarische Darstellungen schnell unübersichtlich und wenig informativ. Im Extremfall kommt jede Ausprägung nur noch genau einmal vor. Häufig taucht dieses Problem bei metrischen Variablen auf. Für solche Merkmale müssen die Werte zunächst gruppiert (kategorisiert) werden, damit die beobachteten Häufigkeiten für jede Kategorie aufgeführt werden können. Natürlich geht damit immer auch ein Informationsverlust einher.
Tabellarische Darstellung von Mehrfachnennungen
Es ist plausibel, dass je nach Fragestellungsperspektive bei (kategorialen) Merkmalen auch mehr als eine Ausprägung pro Beobachtung vorliegen kann. Zum Beispiel werden in Fragebögen häufig Listen von Kategorien abgefragt ("Welche Haustiere gibt es in Ihrem Haushalt?"), bei denen die Befragten explizit darauf hingewiesen werden, dass "Mehrfachantworten" zulässig sind (man kann ja Hunde und Katzen besitzen). Für die tabellarische Darstellung ergibt sich hier das Problem, auf welche "Gesamtheit" sich Anteile und Prozentangaben beziehen sollen: Die Anzahl der Befragten oder die Anzahl der insgesamt genannten Kategorien?
Praktische Umsetzung mit Statistiksoftware
In diesem Abschnitt zeigen wir, wie die besprochenen Tabellen mit Statistiksoftware erstellt werden können.
Beispieldaten herunterladen: dat.csv
Datenbeispiel
Unser Beispieldatensatz (hypothetisches Datenbeispiel) liegt als CSV-Datei vor. Die Daten können mit der read.csv-Funktion eingelesen werden (der korrekte Pfad zum Speicherort muss angegeben werden):
dat <- read.csv("C:/... Pfad .../dat.csv")Die Funktion erzeugt ein Objekt vom Typ data.frame, dem wir links vom Zuweisungspfeil (<-) den Namen "dat" geben.
Der Datensatz enthält u.a. die Variablen punkte (erzielte Punktzahl in einem Test), schlafdauer (Schlafdauer in der Nacht vor dem Test in Std.), lernzeit (insgesamt für den Test aufgewendete Lernzeit in Std.) und lsport (Lieblingssportart). Einzelne Variablen können als Datensatzname$Variablenname angesprochen werden, z.B.:
dat$punkte
[1] 93.0 76.5 79.5 85.0 66.5 71.0 56.5 77.0 59.0 63.5 72.0 70.0 96.0 72.0 62.5 76.5 86.0 57.5
[19] 60.0 73.5 64.5 54.0 85.0 64.0 57.5 54.0 76.5 41.0 58.5 87.5 62.5 62.5 100.5 86.0 66.5 79.5
[37] 77.0 67.5 58.5 92.5 94.5 77.0 76.0 67.0 44.5 86.5 70.0 81.5 90.5 78.0 80.5 74.0 56.5 60.0
[55] 83.0 70.0 49.0 57.0 48.0 70.5 96.5 106.0 65.5 86.5 87.5 89.5 64.0 86.0 62.0 94.5 52.0 73.5
[73] 77.0 83.5 62.5 52.5 51.5 86.5 70.5 57.5 68.0 103.0 79.0 75.0 113.5 78.0 104.5 84.5 63.5 46.0
[91] 102.5 77.0 73.5 71.0 106.0 79.0 77.5 87.0 92.5 11.5 83.5 86.5 78.5 67.5 71.0 61.5 31.0 50.5
[109] 87.5 66.5 67.0 60.5 61.5 83.5 66.0 97.0 79.5 83.5 82.0 63.0Die Ausgabe zeigt die 120 beobachteten Werte der Variable punkte.
Für einen ersten Überblick über die Struktur des Datensatzes und die im Datensatz enthaltenen Variablen kann die Funktion str(dat) verwendet werden:
str(dat)Diese liefert das folgende Ergebnis:
'data.frame': 120 obs. of 25 variables:
$ X : int 94 66 78 28 3 113 16 11 96 99 ...
$ punkte : num 93 76.5 79.5 85 66.5 71 56.5 77 59 63.5 ...
$ schlafdauer : num 6.2 5.3 5.5 7 6.5 6.4 5.7 6.8 5.4 6.8 ...
$ lernzeit : num 8.2 7 6.8 7.3 7.3 3.9 4.9 7.6 2.5 9.2 ...
$ nachhilfe : int 1 1 1 1 1 0 0 1 0 0 ...
$ zeugnis_mathe_roh : num 101.3 89.7 86.2 83.6 86.8 ...
$ zeugnis_mathe_punkte : int 13 11 10 10 10 11 9 10 9 10 ...
$ zeugnis_mathe_note : Factor w/ 4 levels "ausreichend",..: 1 2 2 2 2 2 3 2 3 2 ...
$ zeugnis_deutsch_punkte: int 8 9 10 6 10 10 9 12 5 13 ...
$ zeugnis_deutsch_note : Factor w/ 4 levels "ausreichend",..: 3 3 2 4 2 2 3 2 4 1 ...
$ lsport : Factor w/ 6 levels "Andere Sportart",..: 4 5 1 3 3 4 3 3 4 4 ...
$ sport_fb : int 0 1 0 1 1 1 1 1 1 1 ...
$ sport_bb : int 0 0 1 0 0 0 0 1 1 0 ...
$ sport_sw : int 1 1 1 1 0 0 1 1 1 1 ...
$ sport_tn : int 0 0 0 0 0 0 0 0 1 0 ...
$ sport_an : int 1 0 1 1 0 0 1 1 1 1 ...
$ sport_no : int 0 0 0 0 0 0 0 0 0 0 ...
$ sport_test : int 0 1 1 0 1 1 0 1 1 1 ...
$ kantine_zufr : int 4 4 3 5 3 2 2 1 3 2 ...
$ taschengeld : int 33 30 29 35 28 32 41 36 34 34 ...
$ lauf100 : num 14.3 13.2 13.9 14 15 14.2 14.1 14.8 15.2 13.8 ...
$ lauf1000 : num 234 229 210 222 227 ...
$ lauf5000 : num 489 465 484 486 461 ...
$ kugel : num 8.15 9.26 8.47 8.37 7.56 ...
$ lfach : Factor w/ 7 levels "anderes Fach",..: 2 2 2 2 2 2 2 2 2 2 ...Zu den einzelnen Variablen zeigt die Ausgabe deren Speicherformat (int für "integer", num für "numeric" — beides Zahlenwerte, Factor für nicht-numerische Variablen) und die jeweils ersten Werte im Datensatz.
In der Benutzeroberfläche R-Studio liefert der Data Viewer zudem einen Einblick in den Datensatz als Datentabelle. Aufgerufen wird er mit der Funktion
View(dat)So sieht ein Ausschnitt aus dem Data Viewer aus:
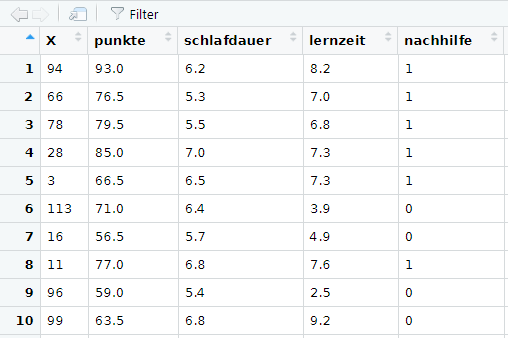
Tabellen
Für eine einfache Häufigkeitstabelle verwenden wir die Funktion table():
> table(dat$lsport)
Andere Sportart Basketball Fußball Keine Sportart
14 18 34 32
Schwimmen Tennis
16 6 Relative Häufigkeiten erhalten wir mit der Funktion prop.table():
> prop.table(table(dat$lsport))
Andere Sportart Basketball Fußball Keine Sportart
0.1166667 0.1500000 0.2833333 0.2666667
Schwimmen Tennis
0.1333333 0.0500000 Kumulierte Anteile können wir uns mit der Funktion cumsum() anzeigen lassen:
> cumsum(prop.table(table(dat$kantine_zufr)))
1 2 3 4 5
0.09243697 0.41176471 0.65546218 0.88235294 1.00000000 Bei einem Merkmal mit sehr vielen Ausprägungen — wie etwa punkte — bietet eine Häufigkeitstabelle keine gute Übersicht über die Verteilung. Wir erstellen eine neue Variable punkte_kat, die eine kategorisierte Version der Variable punkte darstellt. Dazu teilen wir die Variable punkte mit der Funktion cut() in Gruppen mit definierten Grenzen auf. Mit breaks definieren wir die Grenzen und mit labels geben wir den gebildeten Gruppen Bezeichnungen:
> dat$punkte_kat <- cut(dat$punkte,
+ breaks = c(0,19.9,39.9,59.9,79.9,99.9,120),
+ labels = c("0-19,5",
+ "20-39,5",
+ "40-59,5",
+ "60-79,5",
+ "80-99,5",
+ "100-120"))
> table(dat$punkte_kat)
0-19,5 20-39,5 40-59,5 60-79,5 80-99,5 100-120
1 1 20 59 32 7 Diagramme für nominale und ordinale Merkmale
Balken- und Säulendiagramme
Nominale und ordinale Merkmale lassen sich grafisch mit Balken- bzw. Säulendiagrammen oder Kreisdiagrammen darstellen. Für Balken-/Säulendiagramme wird für jede Ausprägung ein Balken (eine Säule) eingezeichnet. Die Länge des Balkens (die Höhe der Säule) repräsentiert die (entweder absolute oder relative) Häufigkeit der Ausprägung. Der Informationsgehalt ist damit identisch mit dem einer Tabelle mit absoluten/relativen Häufigkeiten.
Kreisdiagramme
Kreisdiagramme stellen relative Häufigkeiten übersichtlich dar. Der gesamte Kreis stellt 100% der Fälle dar. Für jede Ausprägung wird ein (Torten-)Stück des Kreises in der Größe der relativen Häufigkeit eingezeichnet.
Kreisdiagramme eignen sich gut, um den Bezug zu einer "Gesamtheit" darzustellen. Sie sind weniger gut geeignet, wenn das Merkmal viele und teilweise nur sehr selten vorkommende Ausprägungen besitzt.
Diagramme für metrische Merkmale
In einem Säulendiagramm können die Säulen auf der x-Achse prinzipiell beliebig platziert werden. Metrische Merkmale lassen sich dagegen auf einer mit einer Skala versehenen Achse abtragen. Die Häufigkeit der verschiedenen Merkmalsausprägungen lassen sich dann auf unterschiedliche Weise darstellen.
Histogramme
Für ein Histogramm wird für einzelne Abschnitte der Merkmalsausprägung ein Rechteck gezeichnet, dessen Fläche der Anzahl der Beobachtungen mit Ausprägungen in diesem Abschnitt entspricht. In der Regel werden Abschnitte mit gleicher Breite gewählt — die Darstellung ähnelt dann einem Säulendiagramm ohne Abstände zwischen den Säulen. Genauso können aber auch unterschiedlich breite Abschnitte gewählt werden. Je nachdem, wie viele Abschnitte eingezeichnet werden, wird die Verteilung detaillierter dargestellt oder stärker zusammengefasst.
Dichteplots
Dichteplots stellen eine Möglichkeit dar, die in Histogrammen notwendige Einteilung des Merkmals in einzelne Abschnitte zu vermeiden. Anstelle der Häufigkeiten der Ausprägungen wird das Ergebnis einer komplexeren Berechnung abgetragen, der sogenannte "Kerndichteschätzer". Die Verteilung wird damit als Dichtekurve dargestellt.
Die Dichte ist allgemein definiert als \( Dichte = \frac{relative~Häufigkeit}{Klassenbreite} \). Das heißt, dass Flächen unter einem bestimmten Bereich der Dichtekurve immer der Häufigkeit von Merkmalsausprägungen in diesem Bereich der Verteilung entsprechen. Die Gesamtfläche unter der Kurve ist 1.
Je nach Wahl der genauen Berechnungsart können Kurven entstehen, die mehr oder weniger von den Rohdaten abstrahieren — ähnlich wie im Histogramm unterschiedlich viele Abschnitte abgetragen werden können. Eine "weniger genaue" Abbildung kann den Vorteil haben, die wesentlichen Merkmale der Verteilung herauszustellen, auch wenn Details verloren gehen.
Häufigkeit, relative Häufigkeit und Dichte in Histogrammen
In diesem Abschnitt zeigen wir verschiedene Möglichkeiten, die y-Achse eines Histogramms zu spezifizieren.
Boxplots
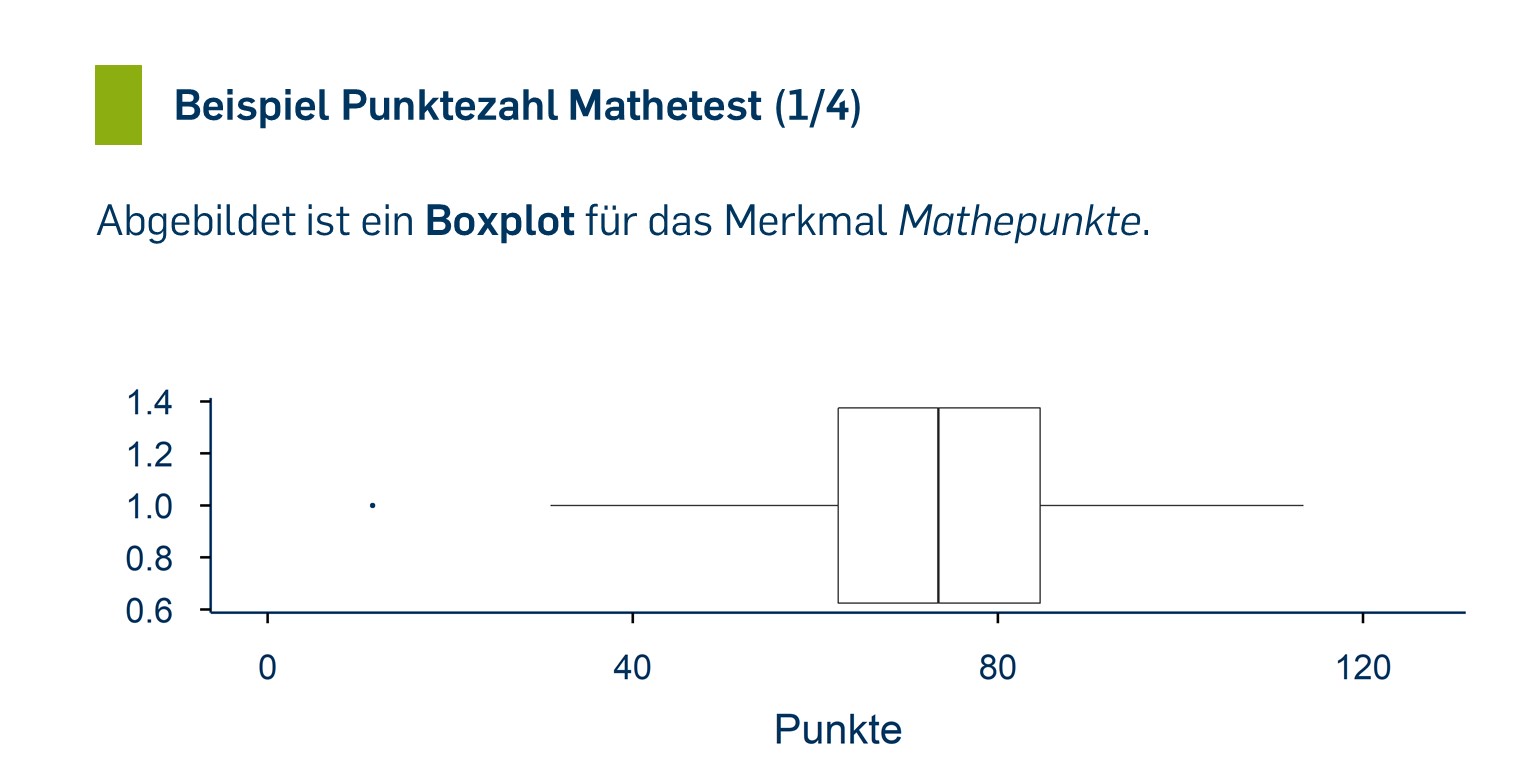
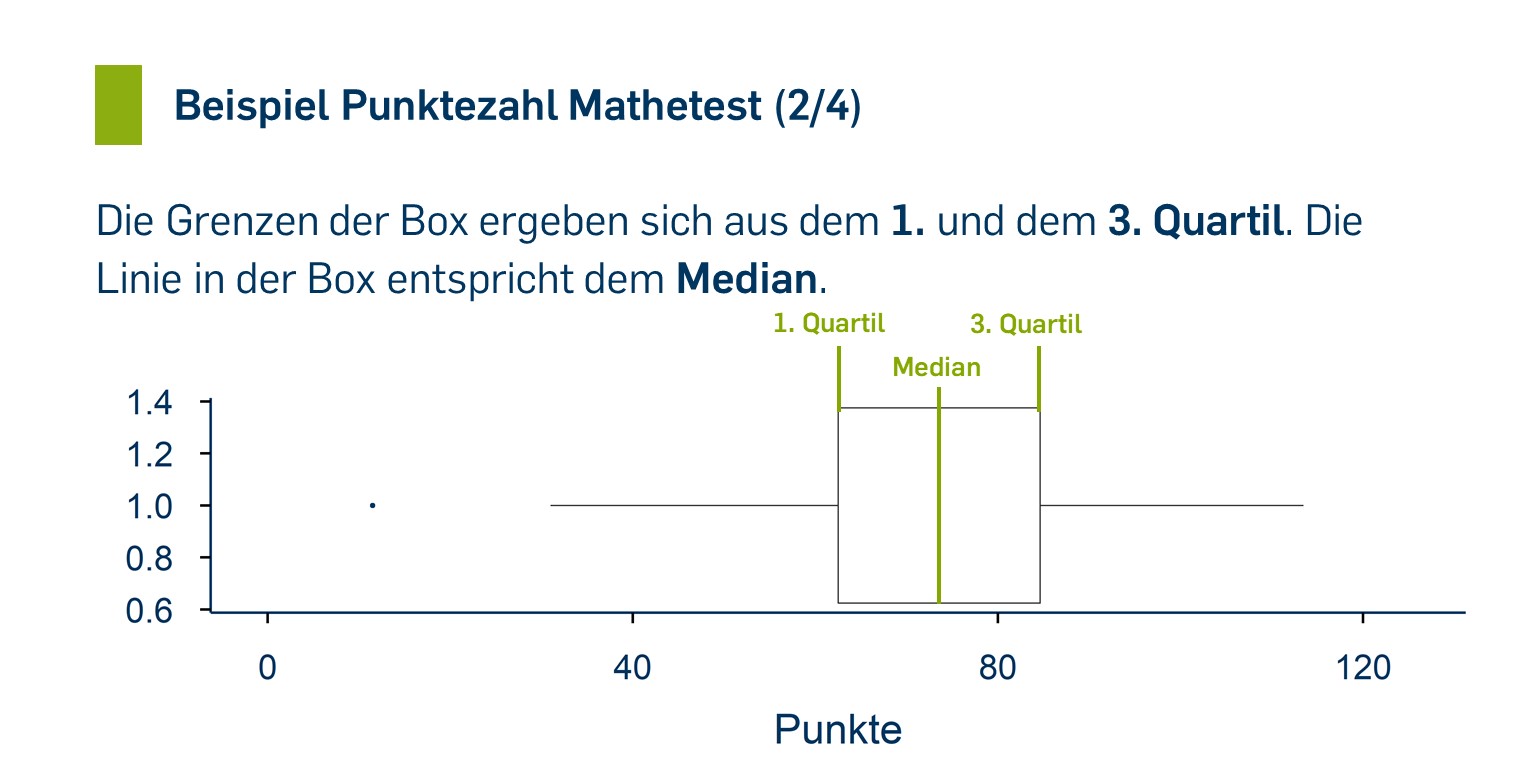
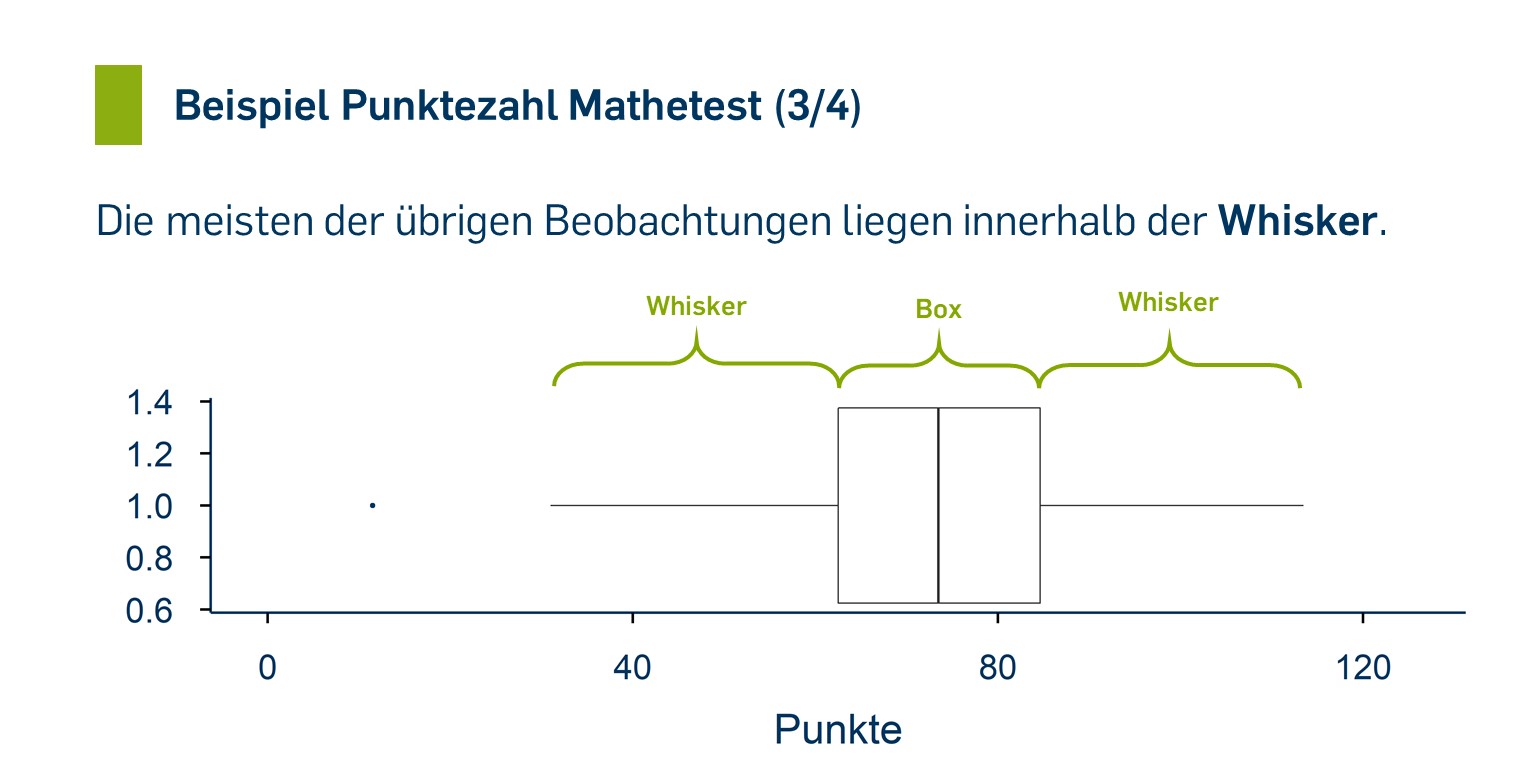
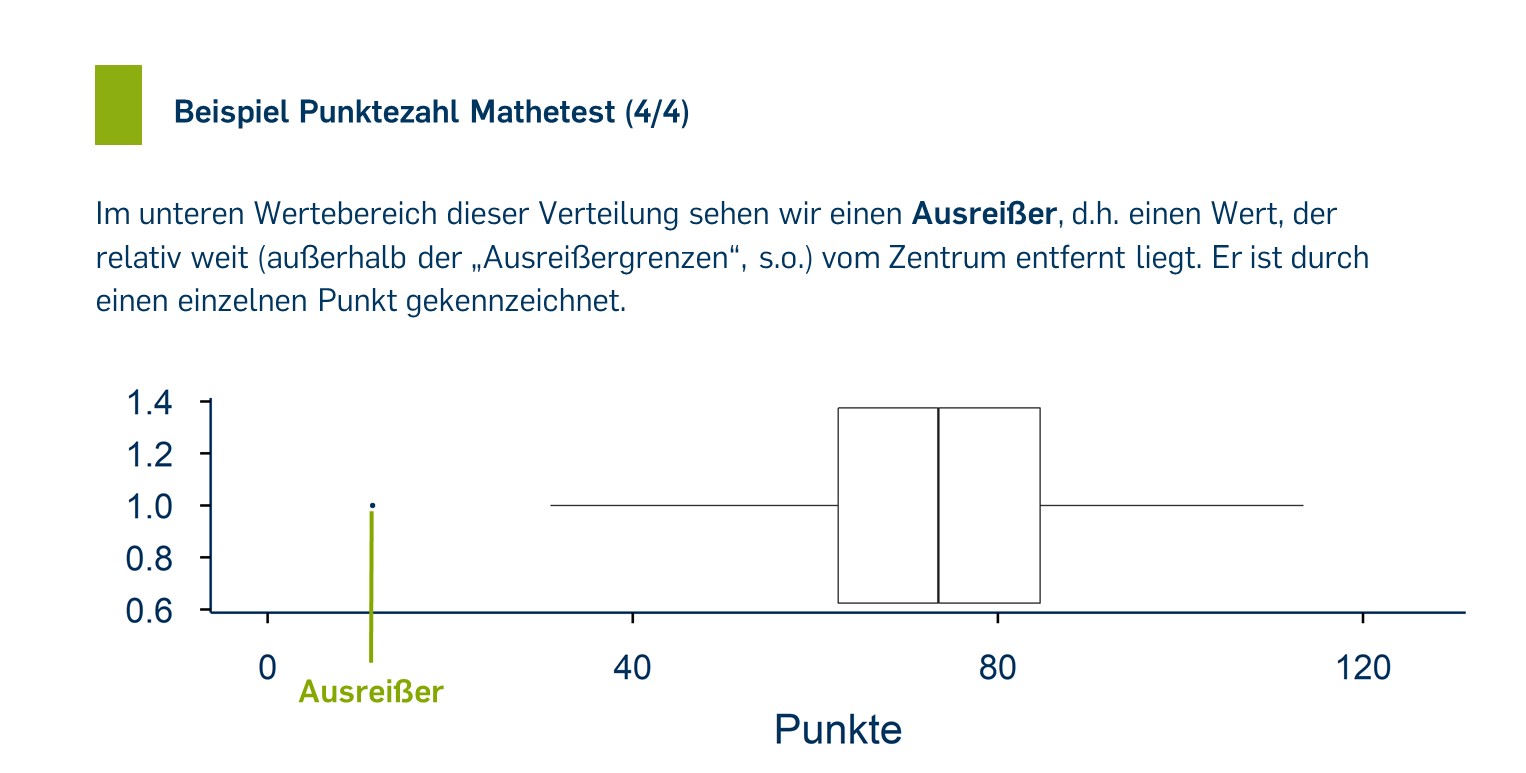
Boxplots (auch Box-and-Whisker-Plots) bilden die Verteilung durch eine grafische Darstellung von Lagemaßen [Link Lagemaße] ab: Eingezeichnet werden als "Box" das 1. und das 3. Quartil und der Median als Linie in dieser Box. Die "Whisker" zeigen an, in welchem Bereich die übrigen Beobachtungen liegen. "Ausreißer"-Werte, die relativ weit von der zentralen Lage der Verteilung entfernt liegen, werden häufig als separate Punkte eingezeichnet — die Whisker reichen dann jeweils bis zur letzten empirisch vorkommenden Beobachtung vor der "Ausreißergrenze".
Wie weit ein Punkt von der zentralen Lage der Verteilung entfernt sein muss, um als "Ausreißer" zu gelten, ist keine statistisch beantwortbare Frage, sondern eine prinzipiell willkürliche Entscheidung. Als Konvention werden häufig alle Werte, die weiter als das anderthalbfache des Interquartilsabstands (drittes Quartil – erstes Quartil, also die Länge der Box) über dem dritten Quartil oder unter dem ersten Quartil liegen als Ausreißer bezeichnet.
Plots im Vergleich
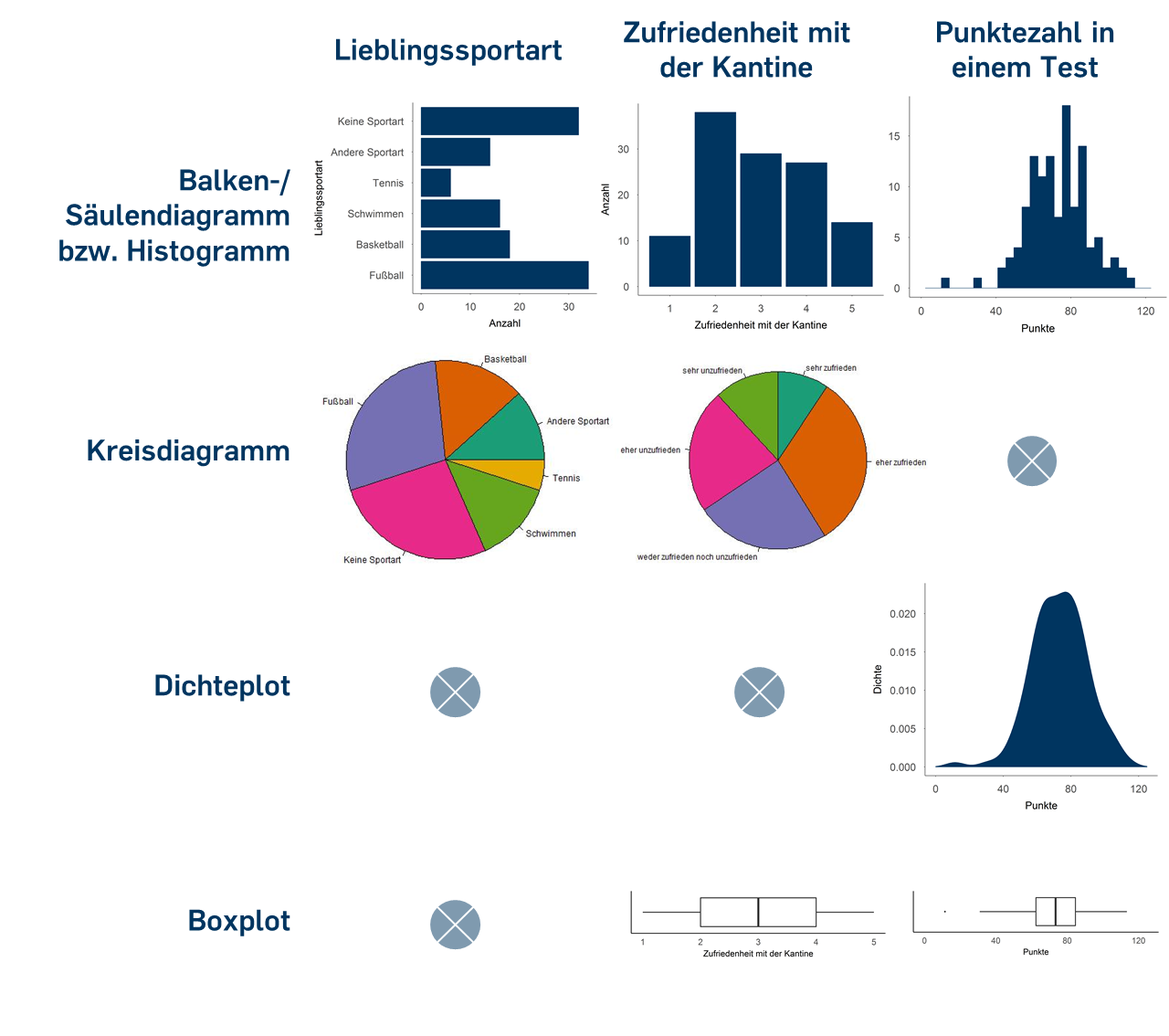
Praktische Umsetzung mit Statistiksoftware
Beispieldaten herunterladen: dat.csv
Datenbeispiel
Unser Beispieldatensatz (hypothetisches Datenbeispiel) liegt als CSV-Datei vor. Die Daten können mit der read.csv-Funktion eingelesen werden (der korrekte Pfad zum Speicherort muss angegeben werden):
dat <- read.csv("C:/... Pfad .../dat.csv")Die Funktion erzeugt ein Objekt vom Typ data.frame, dem wir links vom Zuweisungspfeil (<-) den Namen "dat" geben.
Der Datensatz enthält u.a. die Variablen punkte (erzielte Punktzahl in einem Test), schlafdauer (Schlafdauer in der Nacht vor dem Test in Std.), lernzeit (insgesamt für den Test aufgewendete Lernzeit in Std.) und lsport (Lieblingssportart). Einzelne Variablen können als Datensatzname$Variablenname angesprochen werden, z.B.:
dat$punkte
[1] 93.0 76.5 79.5 85.0 66.5 71.0 56.5 77.0 59.0 63.5 72.0 70.0 96.0 72.0 62.5 76.5 86.0 57.5
[19] 60.0 73.5 64.5 54.0 85.0 64.0 57.5 54.0 76.5 41.0 58.5 87.5 62.5 62.5 100.5 86.0 66.5 79.5
[37] 77.0 67.5 58.5 92.5 94.5 77.0 76.0 67.0 44.5 86.5 70.0 81.5 90.5 78.0 80.5 74.0 56.5 60.0
[55] 83.0 70.0 49.0 57.0 48.0 70.5 96.5 106.0 65.5 86.5 87.5 89.5 64.0 86.0 62.0 94.5 52.0 73.5
[73] 77.0 83.5 62.5 52.5 51.5 86.5 70.5 57.5 68.0 103.0 79.0 75.0 113.5 78.0 104.5 84.5 63.5 46.0
[91] 102.5 77.0 73.5 71.0 106.0 79.0 77.5 87.0 92.5 11.5 83.5 86.5 78.5 67.5 71.0 61.5 31.0 50.5
[109] 87.5 66.5 67.0 60.5 61.5 83.5 66.0 97.0 79.5 83.5 82.0 63.0Die Ausgabe zeigt die 120 beobachteten Werte der Variable punkte.
Für einen ersten Überblick über die Struktur des Datensatzes und die im Datensatz enthaltenen Variablen kann die Funktion str(dat) verwendet werden:
str(dat)liefert das folgende Ergebnis:
'data.frame': 120 obs. of 25 variables:
$ X : int 94 66 78 28 3 113 16 11 96 99 ...
$ punkte : num 93 76.5 79.5 85 66.5 71 56.5 77 59 63.5 ...
$ schlafdauer : num 6.2 5.3 5.5 7 6.5 6.4 5.7 6.8 5.4 6.8 ...
$ lernzeit : num 8.2 7 6.8 7.3 7.3 3.9 4.9 7.6 2.5 9.2 ...
$ nachhilfe : int 1 1 1 1 1 0 0 1 0 0 ...
$ zeugnis_mathe_roh : num 101.3 89.7 86.2 83.6 86.8 ...
$ zeugnis_mathe_punkte : int 13 11 10 10 10 11 9 10 9 10 ...
$ zeugnis_mathe_note : Factor w/ 4 levels "ausreichend",..: 1 2 2 2 2 2 3 2 3 2 ...
$ zeugnis_deutsch_punkte: int 8 9 10 6 10 10 9 12 5 13 ...
$ zeugnis_deutsch_note : Factor w/ 4 levels "ausreichend",..: 3 3 2 4 2 2 3 2 4 1 ...
$ lsport : Factor w/ 6 levels "Andere Sportart",..: 4 5 1 3 3 4 3 3 4 4 ...
$ sport_fb : int 0 1 0 1 1 1 1 1 1 1 ...
$ sport_bb : int 0 0 1 0 0 0 0 1 1 0 ...
$ sport_sw : int 1 1 1 1 0 0 1 1 1 1 ...
$ sport_tn : int 0 0 0 0 0 0 0 0 1 0 ...
$ sport_an : int 1 0 1 1 0 0 1 1 1 1 ...
$ sport_no : int 0 0 0 0 0 0 0 0 0 0 ...
$ sport_test : int 0 1 1 0 1 1 0 1 1 1 ...
$ kantine_zufr : int 4 4 3 5 3 2 2 1 3 2 ...
$ taschengeld : int 33 30 29 35 28 32 41 36 34 34 ...
$ lauf100 : num 14.3 13.2 13.9 14 15 14.2 14.1 14.8 15.2 13.8 ...
$ lauf1000 : num 234 229 210 222 227 ...
$ lauf5000 : num 489 465 484 486 461 ...
$ kugel : num 8.15 9.26 8.47 8.37 7.56 ...
$ lfach : Factor w/ 7 levels "anderes Fach",..: 2 2 2 2 2 2 2 2 2 2 ...Zu den einzelnen Variablen zeigt die Ausgabe deren Speicherformat (int für "integer", num für "numeric" - beides Zahlenwerte, Factor für nicht-numerische Variablen) und die jeweils ersten Werte im Datensatz.
In der Benutzeroberfläche R-Studio liefert der Data Viewer zudem einen Einblick in den Datensatz als Datentabelle. Aufgerufen wird er mit der Funktion
View(dat)So sieht ein Ausschnitt aus dem Data Viewer aus:

Diagramme
Ein Säulendiagramm erstellen wir mit der Funktion barplot(). Da wir die Häufigkeiten der einzelnen Ausprägungen abbilden möchten, geben wir der Funktion nicht die Variable direkt, sondern die Häufigkeitstabelle der Variable, also table(dat$lsport):
barplot(table(dat$lsport))Für ein Säulendiagramm verwenden wir die zusätzliche Option horiz=T:
barplot(table(dat$lsport), horiz=T)Ein Kreisdiagramm erstellen wir mit der Funktion pie(). Mit der Option clockwise bestimmen wir die Richtung der Anordnung:
pie(table(dat$lsport), clockwise = T)Mit der Funktion hist() erstellen wir Histogramme:
hist(dat$punkte)Einen Dichteplot erzeugen wir folgendermaßen: Zuerst wird die Dichtefunktion mit density() berechnet, welche anschließend abgebildet wird mit plot():
plot(density(dat$punkte))Mit boxplot() erzeugen wir ein Boxplot. Mit der Option horizontal = T wird die Box gedreht, also horizontal dargestellt.
boxplot(dat$punkte, horizontal = T)Gestaltungsoptionen
Die gezeigten Diagramme können beliebig gestaltet werden, z.B. folgendermaßen:
hist(dat$punkte,
main = "Histogramm Punktezahl", # Titel
xlab = "Punktezahl", # Beschriftung x-Achse
ylab = "Häufigkeit", # Beschriftung y-Achse
bty = "c" # Art der Umrandung
)Darüber hinaus existieren viele weitere Gestaltungsmöglichkeiten. Wie ein Diagramm sinnvoll zu gestalten ist, hängt von der jeweiligen Verteilung und von der Fragestellung ab.
Diagramme speichern
Die aktuelle Grafik können wir mit der Funktion savePlot() in eine Datei speichern. Dabei sind verschiedene Dateitypen möglich, z.B. PNG oder PDF Der Pfad zum Speicherort muss angepasst werden:
savePlot(filename = "C:/... Pfad .../hist_punkte.png", type = "png")
savePlot(filename = "C:/... Pfad .../hist_punkte.pdf", type = "pdf")Alternativ kann mit pdf() oder mit png() eine Datei erstellt werden und anschließend das Diagramm erzeugt und damit in die Datei geschrieben werden. Abschließend wird die Datei mit dev.off() geschlossen.
pdf("hist_punkte.pdf")
hist(dat$punkte)
dev.off()oder
png("hist_punkte.png")
hist(dat$punkte)
dev.off()Die Größe der Abbildung kann mit den Optionen width und height definiert werden. Bei dem PDF werden die Angaben in inches gemacht, z.B. wird folgendermaßen eine 5 inches breite und 4 inches hohe Abbildung gespeichert:
pdf("hist_punkte.pdf", width = 5, height = 4)
hist(dat$punkte)
dev.off()Bei einem PNG werden Breite und Höhe stattdessen in Pixeln angegeben. Die folgende Abbildung ist beispielsweise 420 Pixel breit und 240 Pixel hoch:
png("hist_punkte.png", width = 420, height = 240)
hist(dat$punkte)
dev.off()