Determinationskoeffizient
Wie gut beschreibt das Modell die Daten?
Mit der Steigung und dem Achsenabschnitt der Regressionsgeraden haben wir bereits zwei wesentliche Punkte, um die Art des Zusammenhangs in unserem Datenbeispiel zu beschreiben. Ein wichtiger Aspekt fehlt aber noch: Wie gut beschreibt die gefundene Gerade die beobachteten Daten? Liegen wir mit den geschätzten \( y \)-Werten nah an den beobachteten \( y \)-Werten, oder weichen die Beobachtungen stark von der Regressionsgeraden ab?
Die folgende Grafik zeigt Beispiele für unterschiedlich "gut beschriebene" Zusammenhänge. Obwohl die Regressionsgeraden teilweise identisch sind, unterscheiden sich die Zusammenhänge deutlich.
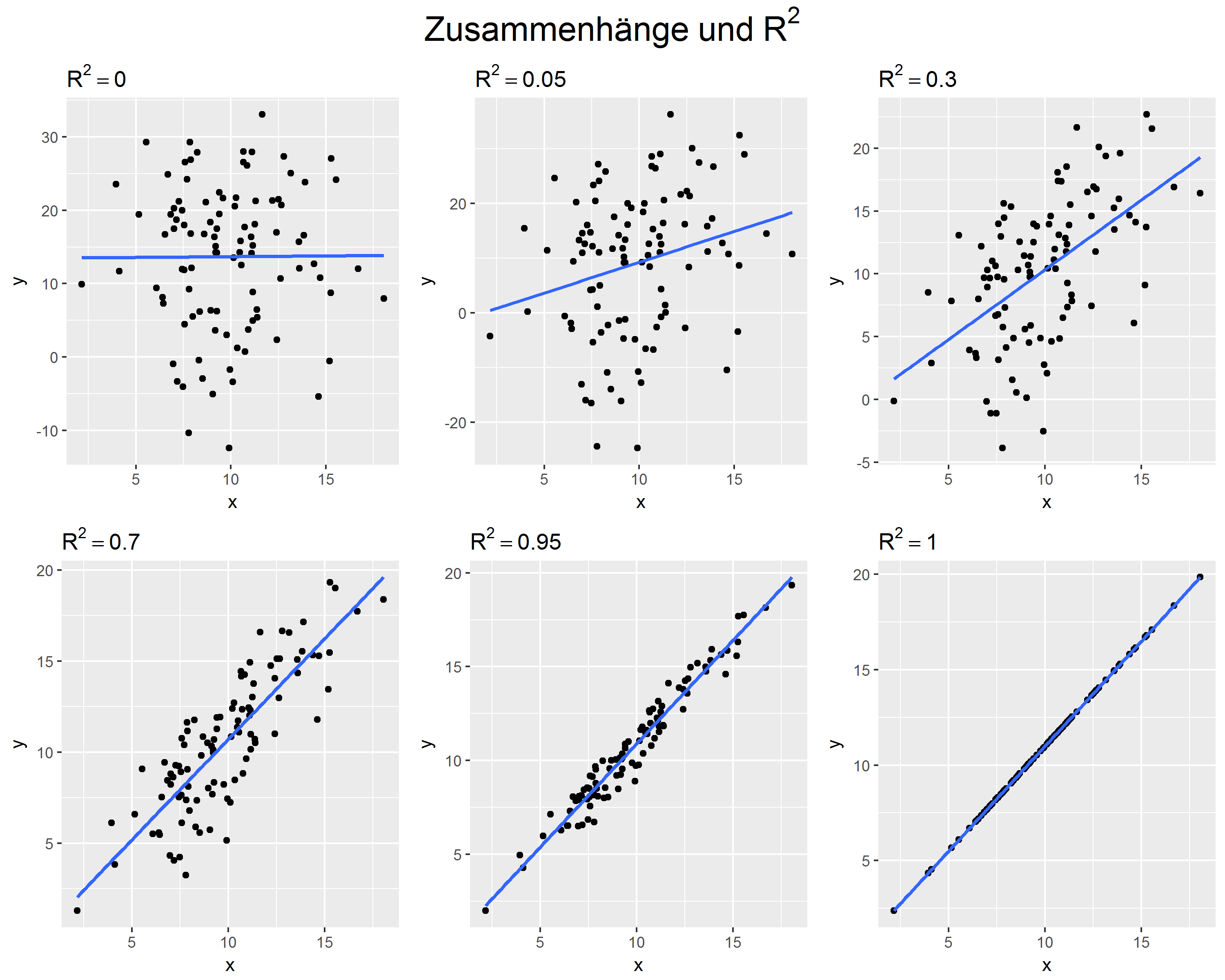
Diesen Aspekt des Zusammenhangs zwischen den Variablen beschreibt der Determinationskoeffizient \( R^2 \) . \( R^2 \) kann Werte zwischen 0 und 1 annehmen. Der Wert kann interpretiert werden als der Anteil der Unterschiede der Werte der abhängigen Variable, der durch die unabhängigen Variablen erklärt werden kann:
- \( R^2=0 \): Die unabhängigen Variablen können \( y \) überhaupt nicht erklären - in diesen Fall finden wir auch keine Steigung der Regressionsgeraden, also alle \( b_k=0 \).
- \( R^2=1 \): Die unabhängigen Variablen erklären \( y \) vollständig - alle beobachteten \( y \)-Werte liegen auf der Regressionsgeraden
- \( R^2=0,7 \): Die unabhängigen Variablen erklären 70% der Unterschiede in \( y \) - 30% der Unterschiede können wir nicht erklären.
In unserem Beispiel erklärt die Schlafzeit 18,6% der Variation der Deutschtest-Ergebnisse, \( R^2 = 0,186 \).
Herleitung von \( R^2 \)
Dieser Abschnitt zeigt, wie \( R^2 \) definiert ist und berechnet werden kann.
Die Grundüberlegung bei der Bestimmung der "Modellgüte" ist, dass ein "besseres" Modell einen größeren Teil der Unterschiede in den Werten der zu erklärenden Variable \( y \) (d.h.: in der Varianz von \( y \)) erklärt . Wir können uns diese "erklärte Varianz" als Gegenstück zur Varianz der Fehlerterme \( e_i \) vorstellen: Die "Gesamt"-Varianz" von \( y \) wird in einen erklärten und einen nicht-erklärten Teil zerlegt.
Wir können uns am bivariaten Beispiel der Regression der Punkte im Deutschtest auf die Schlafdauer veranschaulichen, wie diese Varianzaufteilung funktioniert:
\( R^2 \) wird berechnet als Anteil der erklärten Varianz an der Gesamtvarianz:
In unserem Beispiel kommen wir entsprechend auf:
Durch Herauskürzen von \( n \) erhalten wir die in der Literatur häufig zu findende Formel auf Grundlage der "Summen der Abweichungsquadrate":
SSE steht hier für "Sum of Squares Explained", SST für "Sum of Squares Total". Achtung: teilweise wird das Kürzel SSE auch für "Sum of Squares, Errors", also die Fehlerquadrate der Residuen verwendet!
\( R^2 \): Interpretation
\( R^2 \) kann Werte zwischen 0 und 1 annehmen. Bei \( R^2 = 0 \) tragen die erklärenden Variablen nichts zur Erklärung von \( y \) bei - wenn wir einen \( y \)-Wert erraten müssten, würden wir mit dem Mittelwert \( \bar{y} \) am besten abschneiden. Bei \( R^2 = 1 \) wird \( y \) vollständig erklärt - ein deterministisches Modell, bei dem keinerlei Zufallsfehler auftreten.
Für \( R^2 \) lassen sich keine guten "Faustregeln" zur Interpretation formulieren. Welcher Anteil erklärter Varianz als "gut" oder "zufriedenstellend" zu bezeichnen ist, hängt stark von der untersuchten Fragestellung ab. Vermutlich würden wir in einer Untersuchung über Brettspiele erwarten, die Variable "Anzahl gewonnener Spiele Trivial Pursuit" (mit geeigneten Daten zu den benötigten erklärenden Variablen) grundsätzlich besser erklären zu können als die Variable "Anzahl gewonnener Spiele Mensch-Ärgere-Dich-Nicht". Stehen Untersuchungen zu vergleichbaren Fragestellungen zur Verfügung ist es deshalb hilfreich, sich an dort berichteten \( R^2 \)-Werten zu orientieren.
Häufig wird \( R^2 \) auch verwendet, um Regressionsmodelle mit unterschiedlichen erklärenden Variablen zu vergleichen. Die Interpretation von \( R^2 \) richtet sich dann auf die Frage, ob (z.B. durch Hinzuziehen weiterer erklärender Variablen) eine Verbesserung des Modells erzielt werden konnte, ob also ein größerer Teil der Varianz der abhängigen Variable erklärt werden kann.