Quantitative Datenanalyse
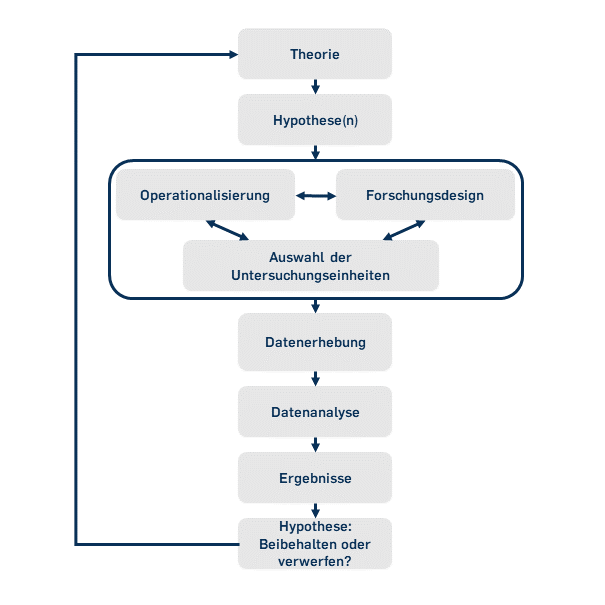
Im Forschungsprozess einer quantitativen Studie stehen die Datenanalyse und die Interpretation der Ergebnisse am Ende eines mehr oder weniger linearen Forschungsprozesses, wie in der Abbildung dargestellt. Wie vorliegende Daten am besten zu analysieren sind, ist daher immer auch eine Frage der bereits getroffenen Entscheidungen im Forschungsprozess.
In diesem Artikel gehen wir auf den Zusammenhang zwischen Theorie und Daten als Grundlage jeder Datenanalyse ein, stellen das wichtige Konzept des Skalenniveaus vor und diskutieren abschließend die Unterscheidung zwischen uni-, bi- und multivariaten Analysen.
Verwendete Beispiele
In allen Artikeln zur quantitativen Datenanalyse - und auch in diesem einleitenden Artikel - verwenden wir als Praxisbeispiel Fragestellungen und Beispieldaten aus dem Kontext einer (hypothetischen) Befragung von Schüler*innen. Ein beispielhafter Datensatz ist hier beschrieben.
Entscheidungen im quantitativen Forschungsprozess
In diesem Abschnitt finden Sie einen kurzen Überblick, welche Fragen sich bei der Datenerhebung, der Auswahl der Untersuchungseinheiten, der Operationalisierung und beim Forschungsdesign stellen können.
Welche Fragen stellen sich im Forschungsprozess vor der Datenanalyse?
Auch wer selbst keine eigenen Daten erheben will, sondern mit vorgefundenen Daten arbeitet, muss beantworten können, wie all diese Entscheidungen getroffen wurden. Denn: Welche Analyeverfahren angemessen sind und wie Analyseergebnisse richtig zu interpretieren sind, hängt maßgeblich von der "Art der Daten", d.h. den Antworten auf die oben gestellten Fragen ab.
Theorie und Daten
Jede quantitative Forschung beginnt mit einer Theorie — nicht nur, wenn explizit eine "theorieprüfende" Untersuchung (s.u.) geplant ist. Eine Theorie besteht aus Aussagen über die Realität und erhebt den Anspruch, einen mehr oder weniger großen Teil eines Phänomenbereichs beschreiben (oder auch erklären) zu können. Um quantitativ forschen zu können, muss die verwendete Theorie nicht zwingend auf hunderten Buchseiten ausgearbeitet vorliegen. Aber: Wir benötigen theoretische Vorstellungen vom untersuchten Gegenstandsbereich, um überhaupt Daten erheben — also messen zu können. Die Theorie muss uns aufzeigen können, "worauf wir schauen müssen".
Konstrukte unterscheiden
Die Theorie beschreibt, welche Aspekte im Gegenstandsbereich relevant/zu unterscheiden/besonders zu beachten sind. Wir sprechen von theoretischen Begriffen oder Konstrukten.
Im nächsten Abschnitt finden sich einige Aussagesätze, die Teil einer Theorie zur "Akzeptanz des Schulessens" sein könnten. Über welche Konstrukte wird hier gesprochen? (Durch Anklicken der (+) können Vorschläge zur Benennung der theoretischen Konstrukte angezeigt werden.)
Ausprägungen identifizieren
Für jedes Konstrukt müssen wir auch eine Vorstellung davon haben, welche Ausprägungen möglich sind, also: Welche unterschiedlichen "Zustände" das Konstrukt bei den einzelnen Untersuchungseinheiten aufweisen kann.
Diese Ausprägungen können verschiedene Formen annehmen. Eigenschaften können vorliegen oder nicht vorliegen; eine von mehreren möglichen Eigenschaften kann zutreffen; andere Merkmale können in unterschiedlichem Ausmaß vorliegen.
Im folgenden Beispiel kann mit dem Schieberegler zwischen Beispielmerkmalen und der Form ihrer Ausprägungen gewechselt werden.
Indikatoren finden
Theoretische Begriffe sind in der Regel nicht direkt beobachtbar. In der Operationalisierung wird unter anderem festgelegt, an welchen beobachtbaren Merkmalen (Indikatoren) das Vorliegen des Konstrukts bzw. einer bestimmten Ausprägung des Konstrukts festzumachen ist.
Betrachten wir als Beispiel das Schüler*innen-Merkmal "Qualität des Verhältnisses zu den Lehrer*innen" (gut – schlecht). Es erscheint plausibel, dass es dieses Merkmal gibt und dass sich Schüler*innen darin unterscheiden. Wir können es den Schüler*innen aber nicht "ansehen" — wir benötigen Indikatoren.
Mögliche beoachtbare Merkmale für die Qualität des Lehrkraft-Schüler*innen-Verhältnisses könnten etwa sein:
- (Wie häufig) unterhalten sich die Schüler*innen mit ihren Lehrkräften über Dinge, die nichts mit dem Unterricht zu tun haben?
- Wie freundlich wird die Lehrkraft begrüßt?
- Oder einfacher: Eine Selbstauskunft der Schüler*innen darüber, wie sie das Verhältnis zu ihren Lehrer*innen bewerten.
Merkposten
Wichtig: Fragestellungen von Forschungsarbeiten enthalten typischerweise mehrere Konstrukte. Vor einer Datenanalyse (natürlich genauso vor einer Datenerhebung) ist es deshalb wichtig, die einzelnen theoretischen Begriffe klar voneinander abzugrenzen und zu überlegen, welche Ausprägungen jeweils auftreten könnten.
Messen
Jedes in der Fragestellung adressierte Konstrukt muss bei den Untersuchungseinheiten einzeln gemessen werden. Messen heißt, dass die Ausprägung des Konstrukts für jede Untersuchungseinheit festgestellt und deren Relation mit einem Wert (i.d.R. einer Zahl) festgehalten wird. Resultat des Messvorgangs ist eine Variable in der festgehalten wird, welcher Messwert bei welcher Untersuchungseinheit festgestellt wird. Üblicherweise werden Variablen als Spalten in einer Tabelle notiert, in der jede Zeile für eine Untersuchungseinheit steht.
Skalenniveaus
Die unterschiedlichen Ausprägungen einer Variable können in unterschiedlichen Relationen zueinander stehen. Geben zwei Schülerinnen als Schlafdauer "4 1/2 Stunden" und "9 Stunden" an, können wir sagen, dass die letztere doppelt so lang geschlafen hat wie die erstere. Wenn die beiden ihre Zufriedenheit mit der Schulkantine auf einer 5er-Skala bewerten sollen (1 "sehr zufrieden", 2 "eher zufrieden", 3 "teils/teils", 4 "eher unzufrieden", 5 "sehr unzufrieden") und dort mit "eher zufrieden" und "eher unzufrieden" antworten, können wir sagen, dass die erstere zufriedener ist. Aber: Wir können nicht sagen, um wie viel zufriedener sie ist, denn wir können die "Menge an Zufriedenheit" nicht quantifizieren, die dafür nötig ist von "eher unzufrieden" auf "zufrieden" zu kommen.
Diese Eigenschaft von Variablen wird als "Skalenniveau" bezeichnet. Wichtig: In beiden Fällen werden Zahlen verwendet, um die Messwerte festzuhalten — die Zahlen sind aber je nach Skalenniveau der Variable unterschiedlich zu interpretieren! Die für die Zufriedenheitsmessung verwendeten Zahlen 1, 2, 3, 4 und 5 dürfen nur hinsichtlich ihrer Rangfolge interpretiert werden (wir wissen, dass 4 größer ist als 2, also eine höhere Zufriedenheit abbildet). Eine 2 oder 4 als Messwert der Schlafdauer darf hingegen als Zählwert der geschlafenen Stunden interpretiert werden, weshalb wir beispielsweise auch Verhältnisse bilden können: 4 ist doppelt so lang wie 2.
Für empirische Datenanalysen werden vier Skalenniveaus unterschieden: Nominal-, Ordinal-, Intervall- und Ratioskala.
2. Ordinalskala
Im Gegensatz zu nominalskalierten Variablen können ordinalskalierte Variablen auch in eine Rangordnung gebracht werden (Merkmalsausprägung "A" > Merkmalsausprägung "B").
3. Intervallskala
Bei intervallskalierten Variablen können sinnvolle Aussagen über die Abstände zwischen zwei Merkmalsauprägungen getroffen werden. Die Variable hat jedoch keinen natürlichen Nullpunkt.
4. Ratioskala (auch: Verhältnisskala)
Ratioskalierte Variablen haben den größtmöglichen Informationsgehalt. Im Gegensatz zu intervallskalierten Merkmalen verfügen sie über einen natürlichen Nullpunkt. Dies erlaubt auch Aussagen über das Verhältnis der Merkmalswerte.
Uni-, bi- und multivariate Analysen
Eine wesentliche Unterscheidung der verschiedenen Verfahren der Datenanalyse ist die Frage, ob Variablen einzeln in den Blick genommen werden sollen (univariate Analysen) oder ob Zusammenhänge zwischen (jeweils) zwei Variablen (bivariate Analysen) oder zwischen drei oder mehr Variablen (multivariate Analysen) betrachtet werden sollen.
Univariate Analysen
Univariate Fragestellungen fragen nach der Verteilung einzelner Variablen in einer Stichprobe oder Gesamtheit von Untersuchungseinheiten.
- Wie ist die Mathematik-Klausur ausgefallen?
- Wie zufrieden sind die befragten Schüler*innen mit ihrer Schulkantine?
- Welche Ergebnisse konnten die Schüler*innen beim Sportfest im Weitwurf, 100m-Lauf und im Hochsprung erzielen?
Mathematik-Klausur
Die Verteilung der Noten in der Klausur ist nichts anderes als die Antwort auf die Frage, welche Noten wie häufig vergeben wurden. Wir könnten diese Verteilung möglichst exakt darstellen wollen — z.B. in einer Tabelle oder Grafik — oder die Beschaffenheit der Verteilung mit Kennzahlen beschreiben. Wir könnten etwa die häufigste Note angeben oder mit der Spannweite beschreiben wie unterschiedlich die Noten ausgefallen sind.
Schulkantine
Auch die Verteilung der Zufriedenheit mit der Schulkantine würden wir mit Tabellen, Grafiken oder Kennzahlen beschreiben. Eine solche Darstellung/Beschreibung hat immer einen deskriptiven Charakter. Hier könnten wir aber beispielsweise auch Vorannahmen über die Verteilung haben: Vielleicht erwarten wir, dass die Schüler*innen alle unzufrieden sind, weil die Qualität des Schulessens in der untersuchten Kantine niedrig eingeschätzt wird — und könnten dann durchaus überrascht sein, wenn wir eine Verteilung finden, die diesen Erwartungen nicht entspricht.
Sportfest
Die Frage(n) zum Sportfest zeigen, dass auch die Analyse mehrerer Variablen univariat erfolgen kann. Ausschlaggebend ist, dass hier keine Fragen zum Zusammenhang der einzelnen Variablen gestellt werden — hier interessieren wir uns zunächst nur für Verteilungen der einzelnen Variablen, jede für sich.
Bivariate Analysen
Bivariate Fragestellungen fragen nach dem Zusammenhang zwischen zwei Variablen:
- Gibt es einen Zusammenhang zwischen den schulischen Leistungen in Deutsch und Mathematik?
- Gibt es einen Zusammenhang zwischen der Schlafdauer vor einer Klausur und der erreichten Note?
- Unterscheidet sich die Zufriedenheit mit der Schulkantine an den untersuchten Schulen?
Mathematik- und Deutschnote
Um einen Zusammenhang wie den zwischen Mathemathik- und Deutschnote zu beschreiben, existieren vielfältige Verfahren von (so genannten Kreuz-)tabellen über grafische Darstellungen bis hin zu statistischen Kennzahlen, die die Art und Stärke des Zusammenhangs zu beschreiben versuchen. Welche Verfahren genau ausgewählt werden sollten, hängt wesentlich von der Art (insbesondere: vom Skalenniveau!) der beiden Variablen ab.
Schlafdauer und Klausurnote
Die Frage nach dem Zusammenhang zwischen Schlafdauer und Klausurnote könnten wir stellen, weil wir in den Ausprägungen der einen Variable (Schlafdauer) eine mögliche Erklärung für die Ausprägungen der anderen (Klausurnote) vermuten. Bivariate Analysen haben häufig eine solche Erklärungskomponente. Wichtig: Zusammenhangsanalysen können nur in ganz bestimmten Fällen kausale Beziehungen nachweisen — z.B. wenn die erklärende Variable von den Forschenden "gesetzt" werden konnte und weitere Bedingungen für ein experimentelles Design erfüllt sind. Werden beide Variablen gleichzeitig — z.B. in einem Fragebogen — erhoben, sind diese Bedingungen nicht erfüllt!
Schulkantine und Schulzugehörigkeit
Die Frage zur Zufriedenheit mit der Schulkantine stellt einen Gruppenvergleich dar: Die Verteilung der Zufriedenheitsangaben wird hier nicht "gepoolt" über alle Schulen, sondern für durch die Schulzugehörigkeit definierte Gruppen von Schüler*innen betrachtet. Auch ein solcher Gruppenvergleich ist eine bivariate Analyse, denn die Frage "Schüler*in welcher Schule?" ist hier ebenfalls eine Variabe.
Multivariate Analysen
Nimmt man zusätzlich weitere Variablen in den Blick, wird die Untersuchung vielfältiger Zusammenhänge möglich. Die folgenden Beispielfragen sollen drei häufige Varianten aufzeigen.
- 1) Bleibt der Zusammenhang zwischen Deutsch- und Mathematiknote bestehen, wenn wir berücksichtigen, wie gern ein*e Schüler*in zur Schule geht?
- 2) Kommt der Zusammenhang zwischen Schlafdauer und Klausurnote dadurch zu Stande, dass die Schlafdauer mit der Konzentrationsfähigkeit einhergeht und die Konzentrationsfähigkeit mit der Klausurnote zusammenhängt?
- 3) Fällt der Zusammenhang zwischen Schlafdauer und Klausurnote umso stärker aus, je besser die Qualität des Schlafs war?
Schulnoten und "Gern zur Schule gehen"
Die erste Frage ist ein typisches Beispiel für eine multivariate Analyse zur Drittvariablenkontrolle. Ein Zusammenhang zwischen Deutsch- und Mathematikleistung könnte entstehen, weil Schüler*innen über alle Fächer hinweg besser oder schlechter abschneiden könnten. Es könnte aber auch sein, dass ein solcher Zusammenhang in Teilen oder ganz aus einer unterschiedlichen schulischen Motivation — hier abgebildet über "gern zur Schule gehen" resultiert, die beide Leistungsmessungen gleichermaßen beeinflusst: Der Zusammenhang könnte "verschwinden", wenn wir nur Schüler*innen mit gleichem Motivationsniveau betrachten.
Schlafdauer, Klausurnote und Konzentrationsfähigkeit
Die zweite Frage ist ein Beispiel für eine Mediationsanalyse, die aufzeigen soll, über welchen Mechanismus eine Variable auf die andere Einfluss nimmt. Wenn wir zeigen können,
- dass mehr Schlaf mit mehr Konzentration einhergeht und auch,
- dass mehr Konzentration mit besseren Noten zusammenhängt,
haben wir zumindest einen möglichen "Wirkmechanismus" gefunden. (Aber Achtung: Auch in diesem Fall haben wir noch keine Kausalität nachgewiesen — es könnte auch ganz andere Erklärungen für die beobachteten Zusammenhänge geben als den vermuteten Mechanismus.)
Schlafdauer, Klausurnote und Schlafqualität
Die dritte Frage ist ein Beispiel für einen sogenannten Interaktionseffekt oder Moderationseffekt. Wir könnten vermuten, dass die Schlafdauer zwar grundsätzlich einen (positiven) Zusammenhang mit der erreichten Note hat, dieser Zusammenhang aber auch umso stärker wird, je besser ein*e Schüler*in in der Nacht vor der Klausur schläft. Wir fragen hier also nach einem Unterschied in der Stärke des Zusammenhangs zwischen zwei Variablen in Abhängigkeit von Ausprägungen einer dritten Variable.











































