Einführung in R
Als R wird sowohl die Programmiersprache für statistische Anwendungen als auch das kostenlose Software-System, das auf diese Sprache zurückgreift, bezeichnet. R wurde 1992 von Ross Ihaka und Robert Gentleman auf Basis der Programmiersprache S entwickelt. Gegenwärtig ist R für Windows-, macOs- und Linux-Distributionen verfügbar.
Im Folgenden wird ein kurzer Überblick über das Einrichten von R und den weit verbreiteten Editor RStudio auf dem eigenen Computer gegeben. Daran anschließend wird die R-Syntax und einige grundlegende Datentypen vorgestellt. Abschließend findet sich noch eine kurze Erläuterung zur Installation und Verwendung von packages, die R um weitere Funktionen ergänzen können.
Überblick
Sowohl die Installation als auch die Verwendung von R ist kostenlos. Da R ein GNU-Projekt (General Public Licence) ist, können seine Nutzer*innen zusätzlich eigene Erweiterungen erstellen oder Erweiterungen aus der R-Community frei nutzen. Parallel dazu wird die Grundstruktur von R durch das R (Development) Core Team beständig weiterentwickelt. Dies hat zur Folge, dass aktuelle Verfahren und Techniken der Statistik häufig zuerst in R umsetzbar sind.
R wird mit Programmiercode in einer Console bedient — anstatt z.B. durch Menüs zu klicken. Für Einsteiger*innen ohne Programmiererfahrung kann dieses Vorgehen abschreckend wirken. Einfache statistische Auswertungen können jedoch schon mit wenigen grundlegenden Funktionen durchgeführt werden. Zahlreiche (Online-)Publikationen erleichtern zudem auch komplexere Analysen.
Einstieg und technische Voraussetzungen
Um mit R auf einem Computer arbeiten zu können, wird eine R-Installation benötigt und eine integrierte Enwicklungsumgebung (IDE — integrated development environment) empfohlen.
Üblicherweise handelt es sich bei letzterem um das kostenlose und opensource RStudio, das von dem gleichnamigen Unternehmen vertrieben wird. (Es können aber auch Alternativen wie Jupyter notebook, Visual Studio, Vim und andere verwendet werden. In dieser Einführung beschränken wir uns jedoch darauf RStudio vorzustellen, da es das verbreitetste IDE für R ist.)
Durch das Installieren von R wird automatisch das Rgui (graphical user interface) mit eingerichtet. In dieser grafischen Benutzeroberfläche kann jeder R-Code eingegeben und ausgeführt werden. Es ist also möglich, alle statistischen Berechnungen mit R allein in dem Rgui durchzuführen.
Wir empfehlen dennoch ein IDE wie RStudio für Analysen mit R. Das Rgui soll lediglich das Arbeiten mit R durch eine grafische Oberfläche ermöglichen. Daneben bietet es kaum weitere Funktionen, die das Programmieren mit R vereinfachen und dadurch beschleunigen. RStudio bietet dagegen Features, die u. a. das Erkennen von Fehlern verbessern, Code-Vorschläge zugänglicher machen und die Übersicht über die Analyseschritte angenehmer gestalten (um hier nur eine ganz kleine Auswahl zu nennen). Aus diesem Grund wird in dieser Einführung hauptsächlich das Arbeiten mit RStudio gezeigt.
Um zu verstehen, wie R und RStudio miteinander interagieren, stellen wir uns vor, dass eine Nutzer*in eine statistische Berechnung mit R durchführen möchte:
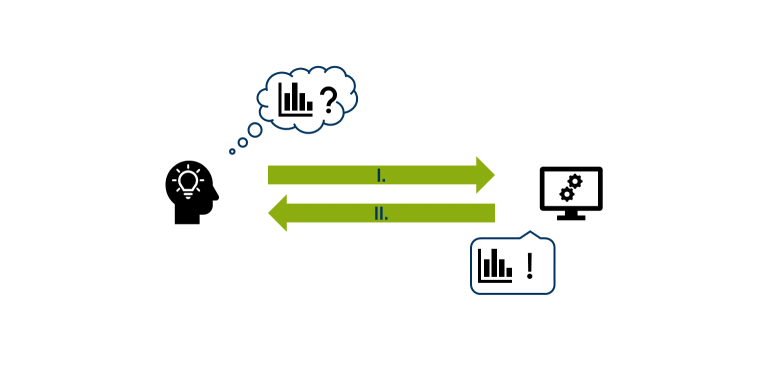
Von Außen betrachtet muss sie dafür lediglich R-Code in einer Benutzeroberfläche (RStudio, Rgui,...) ausführen (I.). Nach der Berechnung des Codes wird ein Ergebnis dargestellt (II.).
In einem solchen Schema wird jedoch unterschlagen, dass in der Benutzoberfäche der Code nicht verarbeitet wird, sondern in dem Prozessor des Computers. Der Prozessor kann jedoch nur Binärcode (bestehend aus 0 und 1) lesen und erzeugen. Es braucht daher eine Instanz, die den R-Code in Binärcode umwandeln kann und umgekehrt. Diese Instanz ist der R-interpreter, der ein Teil der R-Installation ist.
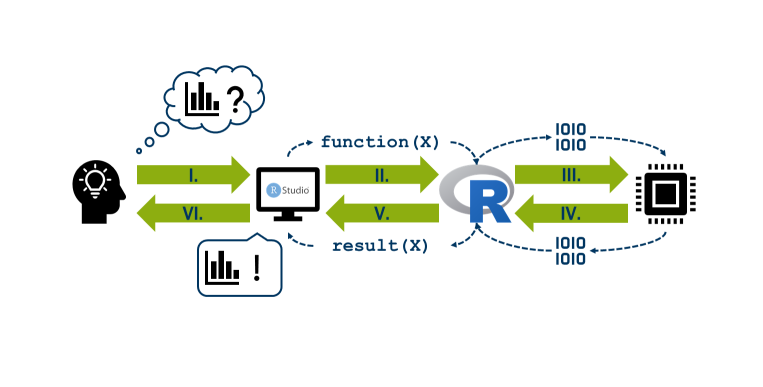
Technisch stellt sich der Weg von der Eingabe zur Ausgabe stark vereinfacht wie folgt dar: Die Nutzer*in schreibt den R-Code in der Benutzeroberfläche (I.). Durch das Ausführen des Codes wird dieser an den R-interpreter geleitet (II.). Dort wird die Anweisung in Binärcode umgewandelt und an den Prozessor gesendet (III.). Hier wird schließlich das Ergebnis der Eingabe berechnet (z.B. eine Zahl, eine Grafik oder eine Fehlermeldung) und anschließend wieder an den R-interpreter in Binärcode übermittelt (IV.) Dieser wandelt den Code wieder um (V.), sodass er in der Benutzeroberfläche dargestellt werden kann (VI.).
Zusammenfassung: Für die Nutzung von R wird eine Benutzeroberfläche benötigt. Dabei muss es sich jedoch nicht RStudio handeln, sondern kann auch das Rgui, ein Terminal oder eine andere Entwicklungsumgebungen sein. Damit der R-Code ausgeführt werden kann, ist der R-interpreter zwingend erforderlich. Oder kurz: R funktioniert ohne RStudio, RStudio jedoch nicht ohne R. Aus diesem Grund empfehlen wir R zuerst zu installieren und dann RStudio.
Installation und Einrichtung von R/RStudio
R und RStudio können nur separat voneinander installiert werden. Im Folgenden wird zuerst die Installation von R und dann von RStudio gezeigt.
Die offizielle R-Installationsanleitung kann auf cran.r-project.org abgerufen werden. Ein Kurzeinführung für RStudio findet sich auf dem github-Profil von RStudio Education.
Windows
Um am schnellsten zu der aktuellsten R-Version zu gelangen, kann die Adresse CRAN MIRROR/bin/windows/base/release.html verwendet werden: Wenn also der Mirror der Universität Münster benutzt wird, ist die Linkadresse https://cran.uni-muenster.de/bin/windows/base/release.html.
Alternativ zu diesem direkten Weg, ist auch eine Auswahl bestimmter Dateien über die CRAN-Webseite möglich — auf diese Weise können die Installationsanleitung, FAQ, ältere Versionen etc. eingesehen werden.
Das folgende Video zeigt den Download der R-Installationsdatei und die Installation von R auf einem Windows-Rechner. Klicke auf die PLUS-Buttons, wenn du zu einzelnen Schritten weitere Informationen erhalten möchtest:
macOS
Um die Installationsdatei für Mac-Betriebssysteme herunterladen zu können, muss die Option Download R for macOS ausgewählt werden.
Der Download des aktuellsten Installations-Package findet sich unter R-4.1.1.pkg (der Name ist versionsabgängig) für macOS 10.13 (High Sierra) oder jünger. R kann jedoch auch auf älteren macOS-Versionen eingerichtet werden (die Links zu den Download-Dateien finden sich ebenfalls auf der Seite).
Nach der Ausführung des Installations-Package muss den Read Me-Informationen und der Lizenzvereinbarung zugestimmt werden (evtl. wird noch nach dem Administrator-Passwort gefragt). Danach beginnt die Installation von R.
Wenn die Installation abgeschlossen ist, muss R zu den Programmen hinzugefügt werden und kann von dort ausgeführt werden.
Linux
Hinweis: Bei manchen Linux-Distributionen ist R bereits vorinstalliert.
Die korrekten Terminal-Befehle für die Installation von R unter Linux-Distributionen finden sich unter Download R for Linux (Debian, Fedora/Redhat, Ubuntu). Nachdem die eigene Linux-Distribution ausgewählt worden ist, können die jeweiligen Terminal-Befehle für die Installation eingesehen werden.
Nach dem Abschluss der Installation kann R mit dem Befehl
$ R
im Terminal gestartet werden.
Starten des Rgui
Klicke auf die PLUS-Buttons, wenn du zu einzelnen Schritten weitere Informationen erhalten möchtest:
Installation von RStudio
Klicke auf die PLUS-Buttons, wenn du zu einzelnen Schritten weitere Informationen erhalten möchtest:
Windows
MacOS
Die Download-Datei für macOS kann im Download-Bereich von rstudio.com unter macOS 10.14+ heruntergeladen werden
Die aktuellste Version von RStudio Desktop setzt macOS 10.13 (High Sierra) oder höher voraus. Für ältere Betriebssysteme können ältere Versionen von RStudio verwendet werden. Nach dem Download der Datei RStudio-2021.09.0-351.dmg (der Name ist versionsabhängig) muss diese installiert werden, evtl. muss dazu das eigene Passwort angegeben werden. Nach dem Beenden der Installation muss RStudio zu den Programmen hinzugefügt werden und kann von dort aus ausgeführt werden.
Linux
Bevor RStudio auf Rechnern mit Linux-Distributionen installiert werden kann, muss je nach Distribution der Public Key von RStudio validiert werden. Eine Anleitung dazu findet sich auf rstudio.com. Die aktuellsten Versionen von RStudio Desktop für Linux-Distributionen setzen ein 64-bit System voraus. Ältere Versionen können jedoch auch verwendet werden. Der Ablauf der Installation ist abhängig von der jeweiligen Distribution. RStudio wird wie andere Programme gestartet.
RStudio
Die Arbeit mit R kann nun komplett in RStudio erfolgen, R muss nicht separat gestartet werden.
In der folgenden Präsentation werden ein paar grundlegende Funktionen von RStudio gezeigt. Eine ausführliche Dokumentation findet sich auf rstudio.com.
Schnelleinstieg in RStudio
Arbeiten mit RStudio
R-Syntax
R ist eine Programmiersprache, die für Statistik-Anwendungen optimiert ist. Sie bringt viele grundlegende Statistikbefehle mit, sodass nicht jede Analyse völlig neu programmiert werden muss. Ihre Syntax legt fest, nach welchen Regeln ihre einzelnen Elemente verwendet werden dürfen.
Code schreiben
R-Code wird von oben nach unten und von links nach rechts ausgeführt — dabei gelten alle Rechenregeln (Punkt vor Strich, Klammern zuerst etc.). Zudem steht jede Eingabe immer in einer einzigen Zeile, außer sie wird durch ein Rechenzeichen am Ende der Zeile offen gehalten (durch eine offene Klammer, ein Plus, ein Divisionszeichen etc.).
Beispiel:
Wir wollen folgende Rechnung in R durchführen: $$3+\frac{6}{10}+2$$
Wir können alle dafür benötigten Zeichen in eine einzige Zeile schreiben und erhalten das korrekte Ergebnis.
> 3 + 6 / 10 + 2
[1] 5.6Es ist ebenfalls möglich, dass jede Zahl in einer einzelnen Zeile steht. Dann müssen die Zeilen am Ende durch ein Rechenzeichen offengehalten werden.
> 3 +
6 /
10 +
2
[1] 5.6Steht das Rechenzeichen am Anfang der Zeile, erhalten wir ein ungewolltes Ergebnis. (Für R ist die Codezeile abgeschlossen und + 2 somit wieder eine neue Codezeile.)
> 3 +
6 /
10
+ 2
[1] 3.6
[1] 2Case-Sensitivität
R ist case-sensitiv — es wird zwischen Groß- und Kleinschreibung unterschieden!
Z.B.: Mit der Eingabe Sys.time() kann die aktuelle Zeit angezeigt werden:
> Sys.time()
[1] "2021-07-14 11:10:29 CEST"Wird stattdessen sys.time() (also ein kleines s) in den Code geschrieben, liefert die Console bei der Ausführung eine Fehlermeldung:
> sys.time()
Error in sys.time() : could not find function "sys.time"Rechnen mit R
Rechenoperatoren
Rechenoperation können in R mit folgenden Zeichen durchgeführt werden:
| Rechenoperation | Zeichen |
|---|---|
| Addition | + |
| Subtraktion | - |
| Multiplikation | * |
| Division | / |
| Potenz | ^ |
| Spektrum | : |
| Quadratwurzel | sqrt() |
| natürlicher Logarithmus | log() |
| Exponent | exp() |
| Skalarprodukt | %*% |
Z.B.:
> 3 + 4
[1] 7> 4^2 / 8
[1] 2> 5 : 12
[1] 5 6 7 8 9 10 11 12> exp(1)
[1] 2.718282Logische Operatoren
Neben Rechenoperatoren können auch logische Operatoren verwendet werden:
| Logischer Operator | Zeichen |
|---|---|
| Gleich | == |
| Ungleich | != |
| Nicht | ! |
| Größer als | > |
| Kleiner als | |
| Größer gleich | >= |
| Kleiner gleich | |
| Und | & |
| Oder | | |
Diese Operatoren können nur eines von zwei Ergebnissen erzielen — sie sind entweder wahr (TRUE) oder unwahr (FALSE):
Es ist wahr, dass 6 nicht 4 entspricht.
> 6 != 4
[1] TRUEEs ist unwahr, dass 9 größer als 10 ist.
> 9 > 10
[1] FALSEEs ist unwahr, dass sowohl 8 als auch 9 gleich 3 hoch 2 sind.
> 8 & 9 == 3^2
[1] FALSEEs ist wahr, dass entweder 8 oder 9 3 hoch 2 entsprechen.
> 8 | 9 == 3^2
[1] TRUEKommentare
Es kann sinnvoll sein, den eigenen Code zu kommentieren, damit dieser zu einem späteren Zeitpunkt und/oder von Dritten nachvollzogen werden kann. Ein Kommentar beginnt immer nach einem "hash" (#). Alles was in der selben Zeile nach dem # folgt, wird von R nicht ausgeführt:
> 31 + 53 # Summe der Lehrer*innen in Schule A und B
[1] 84
> sqrt(100) # * 3
[1] 10Objekte und Funktionen
Zentrale Konzepte bei der Programmierung in R sind Objekte und Funktionen — beide vereinfachen und beschleunigen Analysen in R erheblich. Alle Informationen, die im Laufe einer Berechnung verwendet werden, können in Objekten gespeichert werden. Funktionen erlauben es komplexe Auswertungen mit wenig Code durchzuführen.
Objekte
In Objekte werden Inhalte gespeichert, um sie für die weitere Analyse zu sichern. Die Inhalte des Objektes können sich in ihrer Art und Größe stark unterscheiden — sie können eine einzelne Zahl, ein Datensatz mit mehrere tausend Beobachtungen und Variablen, ein Text, ein Zeitspanne, eine Grafik etc. sein. Wollen wir auf diese Inhalte zurückgreifen, müssen wir lediglich das entsprechende Objekt in unserem Code ansprechen.
Objekte erstellen
Objekte werden immer auf diese gleiche Weise erstellt: Zuerst muss der Name des Objektes festgelegt werden. Dann wird ihm der gewünscht Inhalt zugewiesen (sprich in ihm gespeichert). Eine solche Zuweisung erfolgt immer nach dem selben Schema Name des Objektes <- Inhalt des Objektes.
Beispiel:
Wir wollen die Notenpunkte von drei Schüler*innen im Fach Mathematik miteinander vergleichen. Die erste Schüler*in hat 13 Punkte, die zweite 11 Punkte und die dritte 10 Punkte erzielt. Die "Objekte" sind in diesem Fall die einzelnen Schüler*innen und der Inhalt die jeweiligen Notepunkte:
> SchuelerIn_A <- 13 # erste Schüler*in
> SchuelerIn_B <- 11 # zweite Schüler*in
> SchuelerIn_C <- 10 # dritte Schüler*inObjekte verwenden
Nachdem ein Objekt erstellt wurde, ist es im Workspace (dt. der Umgebung) der aktuellen R-Sitzung gespeichert. Auf die Objekte und ihren Inhalt kann nun wieder zurückgegriffen werden. Hinweis: In RStudio werden die erstellten Objekte in dem Environment-Reiter aufgelistet. Wenn der Name eines Objektes im Code angesprochen wird, wird immer Bezug auf seinen Inhalt genommen:
> SchuelerIn_A # Dem Objekt wurde der Inhalt 13 zugewiesen.
[1] 13
> SchuelerIn_B # Dem Objekt wurde der Inhalt 11 zugewiesen.
[1] 11
> SchuelerIn_C # Dem Objekt wurde der Inhalt 10 zugewiesen.
[1] 10Objektnamen stehen somit auch in Rechnungen stellvertretend für ihren jeweiligen Inhalt.
> SchuelerIn_A - SchuelerIn_B # Differenz der Notenpunkte von Schüler\*in A und B
[1] 2
> SchuelerIn_B < SchuelerIn_C # Überprüfung ob Schüler\in B weniger Punkte erzielt hat als Schüler\*in C
[1] FALSEAus Objekten können wiederum neue Objekte erstellt werden:
# Durchschnittliche Punktzahl
> Durchschnitt_ABC <- (SchuelerIn_A + SchuelerIn_B + SchuelerIn_C) / 3
> Durchschnitt_ABC
[1] 11.33333Benennen von Objekten
Damit es auch bei größeren Datenmengen nicht zu Verwechselungen kommt, ist es ratsam den Objekten sinnvolle Namen zu geben. In unserem Beispiel hätten wir das Objekt "SchuelerIn_A" auch einfach "A", "S1" oder "A_SchuelerIn" nennen können — theoretisch kann jede beliebige Zeichenkette als Objektname verwendet werden. Drei Regeln müssen bei der Benennung von Objekten jedoch beachtet werden:
- Der Objektname darf nicht mit einer Zahl beginnen.
> 1.Rechnung <- 7 + 9*(11 + 5)
Error: unexpected symbol in "1.Rechnung"
> Rechnung_1 <- 7 + 9*(11 + 5)
> Rechnung_1
[1] 151- Der Objektname darf keinen der bereits gezeigten Operatoren enthalten. (Das gilt ebenfalls für Kommata und Leerzeichen)
> Apfel+Birne <- 30 + 12
Error in Apfel + Birne <- 30 + 12 : object 'Apfel' not found
> Apfel Birne <- 30 + 12
Error: unexpected symbol in "Apfel Birne"
> Apfel,Birne <- 30 + 12
Error: unexpected ',' in "Apfel,"
> ApfelBirne <- 30 + 12
> ApfelBirne
[1] 42- Es wird zwischen Groß- und Kleinschreibung unterschieden (siehe case-Sensivität)
> klein <- 1^3
> Klein
Error: object 'Klein' not found
> klein
[1] 1Zusätzlich muss berücksichtigt werden, dass ein Objekt überschrieben werden kann. Es sollte derselbe Name also nicht mehrfach vergeben werden:
> Objekt1 <- 25
> Objekt1 <- 5
> Objekt1
[1] 5Diesen Umstand können wir uns aber auch zunutze machen. Hier wollen wir einen Geldbetrag von Cent in Euro umwandeln:
> Taschengeld <- 2000
> Taschengeld
[1] 2000
> Taschengeld <- Taschengeld/100
> Taschengeld
[1] 20Funktionen
Es wurde bereits gezeigt, dass R mit Hilfe von Operatoren wie ein Taschenrechner verwendet werden kann. In den meisten Fällen werden Statistikprogramme für viel komplexere Aufgaben benötigt. Deren Bearbeitung wird durch Funktionen vereinfacht. Funktionen haben immer denselben Aufbau:
<Name der Funktion>(<Argument_1>,<Argument_2>,...,<Argument_n>)Die Argumente einer Funktion sind ihr Input, das aus ihm ermittelte Ergebnis ihr Output. Der Output ist nicht zwangsläufig eine Zahl, sondern könnte z.B. auch eine Grafik oder ein Wort sein.
Ein paar Funktionen wurden bereits verwendet, ohne sie weiter zu erklären. Schauen wir uns die sqrt() Funktion näher an, mit der Quadratwurzeln berechnet werden können — ihr Input ist der Radikand (eine Zahl ≥ 0) und der Output ihre (positive) Wurzel:
> sqrt(100)
[1] 10
> sqrt(16)
[1] 4
> sqrt(-16)
[1] NaN
Warning message:
In sqrt(-16) : NaNs producedEin Großteil aller Funktionen in R verfügt über weiteren Argumente mit deren Hilfe ihr Output spezifiziert werden kann. Ein simples Beispiel dafür ist die round() Funktion mit der Zahlen gerundet werden können. Standardmäßig wird der Input ganzzahlig gerundet:
> round(10/3)
[1] 3Die Funktion verfügt allerdings über ein weiteres Argument digits =, mit dem die Anzahl der Nachkommastellen manipuliert werden kann:
> round(10/3, digits = 1) # Eine Nachkommastelle
[1] 3.3
> round(10/3, digits = 2) # Zwei Nachkommastellen
[1] 3.33
> round(10/3, digits = 5) # Fünf Nachkommastellen
[1] 3.33333Häufig werden die Namen der Argumente selbst nicht in die Funktion aufgenommen. Um Verwirrung und Fehler zu vermeiden, raten wir gerade am Anfang davon ab:
> round(10/3, 1) # Eine Nachkommastelle
[1] 3.3
> round(10/3, 2) # Zwei Nachkommastellen
[1] 3.33
> round(10/3, 5) # Fünf Nachkommastellen
[1] 3.33333Ja, das Erstellen eigener Funktionen kann das Arbeiten in R erheblich vereinfachen (vor allem bei Operationen die mehrmals durchgeführt werden sollen). Einsteiger*innen mag das Schreiben eigener Funktionen anfangs etwas abschrecken. Aus diesem Grund zeigen wir hier die Möglichkeit die Umrechnungsfunktion der Notenpunkte als Funktion in R zu schreiben. (An dieser Stelle geht es nur darum zu zeigen, was mit der R-Syntax prinzipiell möglich ist. Wie genau die Funktion geschrieben wird, muss nicht nachvollzogen werden.)
Unsere Funktion nennen wir Punkte_Note, ihren Input Note:
Punkte_Note <- function(Note){ # Der Name der Funktion wird mit "<-" zugewiesen.
if (Note >= 13) {return("sehr gut")}
else if (Note >= 10 & Note <= 12) {return("gut")}
else if (Note >= 7 & Note <= 9) {return("befriedigend")}
else if (Note >= 4 & Note <= 6) {return("ausreichend")}
else if (Note >= 1 & Note <= 3) {return("mangelhaft")}
else
return("ungenügend")
}So kann sowohl den Objekten SchuelerIn_A, SchuelerIn_B und SchuelerIn_C als auch anderen Notenpunkten eine Zeugnisnote zugeordnet werden:
> Punkte_Note(SchuelerIn_A)
[1] "sehr gut"
> Punkte_Note(SchuelerIn_B)
[1] "gut"
> Punkte_Note(SchuelerIn_C)
[1] "gut"
> Punkte_Note(14)
[1] "sehr gut"
> Punkte_Note(9)
[1] "befriedigend"
> Punkte_Note(1)
[1] "mangelhaft"Hinweis: Auch bei der Benennung von Funktionen muss zusätzlich beachtet werden, dass sie nicht nach integrierten Funktionen benannt werden können (die Funktion sqrt() kann es nicht zweimal geben).
Datentypen in R
Es wurde schon angedeutet, dass sehr verschiedenartige Informationen in R als Daten verwendet werden können. Die Art der Daten — der sogenannte Datentyp — gibt Auskunft über das Format ihrer Information (handelt es sich um eine Zahl, eine Zeichenkette, eine Funktion, eine Grafik...?) und über die Operationen die auf diese angewendet werden können (ist es möglich die Information zu dividieren oder in einem Balkendiagramm darzustellen oder als Überschrift für eine Tabelle zu verwenden...?).
Wird eine falsche Operation mit einer Information durchgeführt, erzeugt dies entweder unerwünschte Ergebnisse oder eine Fehlermeldung in der R-Console. Es ist daher wichtig, einige grundlegende Datentypen in R zu kennen! Dies ermöglicht es, Fehler zu verhindern und Fehlermeldungen richtig zu interpretieren.
Einschub: Alles ist ein Objekt — jedes Objekt hat einen Inhalt und repräsentiert einen Datentyp!
Sämtliche Berechnungen werden in R mithilfe von Objekten durchgeführt, da in ihnen die dafür notwendigen Informationen gespeichert sind. (Ausgenommen sind hier nur die Rechen- und logischen Operatoren, die keine Funktionen sind.) Für die Arbeitsweise von R ist es unerheblich, ob in einer Codezeile ein selbst erstelltes Objekt wie SchuelerIn_A oder eine 1 verwendet wird — beides sind Objekte.
Jedes Objekt repräsentiert immer einen Datentyp. Dieser ist abhängig vom Inhalt des Objektes, z.B. ist 13 immer eine Zahl und true immer ein Wahrheitswert!
| Name des Objektes | Inhalt | Datentyp |
|---|---|---|
| SchuelerIn_A | 13 | Zahl |
| 1 | 1 | Zahl |
| true | true | boolescher Wert |
Der Datentyp legt fest, welche Operationen mit dem Objekt durchgeführt werden können. Zahlen können z.B. miteinander addiert werden, Wörter hingegen nicht:
> SchuelerIn_A + 1
[1] 14
> "Die erste Schüler_in hat die Note" + "sehr gut."
Error in "Die erste Schüler_in hat die Note" + "sehr gut." :
non-numeric argument for binary operatorDer Datentyp ist nicht nur für die Verwendung von Rechenoperatoren wichtig, sondern auch für Funktionen. Funktionen können nur auf bestimmte Datentypen angewandt werden:
# Nur Zahlen können mit round() gerundet werden.
> round(5/4)
[1] 1
> round("hello")
Error in round("hello") : non-numeric argument to mathematical function
# Nur Zeichenketten können mit strsplit() aufgeteilt werden.
> strsplit("hello", split = "")
[[1]]
[1] "h" "e" "l" "l" "o"
> strsplit(5/4, split = "")
Error in strsplit(5/4, split = "") : non-character argumentWie kann ich den Datentyp eines Objektes ermitteln?
Es gibt in R mehrere Funktionen, um den Datentyp eines Objektes zu bestimmen. Alle verwenden leider minimal unterschiedliche Namen oder Einteilungen.
| Datentyp | mode() | typeof() | class() |
|---|---|---|---|
| Ganze Zahl | numeric | integer | integer |
| Dezimalzahl | numeric | double | numeric |
| Zeichenketten | character | character | character |
| logisch | logical | logical | logical |
| Liste | list | list | list |
| Funktion | function | closure | function |
Im Folgenden verwenden wir die mode() und typeof() Funktion, um den Datentyp eines Objektes zu bestimmen. Oft wird der Begriff Datentyp synonym zu Klasse verwendet. In der Tabelle ist bereits erkennbar, dass hier eine große inhaltliche Schnittmenge herrscht. Um Verwirrung zu vermeiden, werden wir weiterhin nur von Datentypen sprechen.
numeric (Zahlen)
Zahlen haben den Datentyp numeric.
> mode(SchuelerIn_A) # Das Objekt "SchuelerIn_A" hat den Inhalt 13, also ein Zahl.
[1] "numeric"
> mode(23.5) # Bei 23.5 handelt es sich um eine Zahl.
[1] "numeric"
> mode(pi) # "pi" ist die Kreiszahl und somit ebenfalls eine Zahl.
[1] "numeric"double (Dezimalzahlen)
Numerics können sowohl integer (ganze Zahlen) als auch double (Dezimalzahlen) sein. Integer sind Zahlen, die ohne Nachkommastellen gespeichert werden, während double immer mit Nachkommastellen gespeichert werden:
> typeof(SchuelerIn_A)
[1] "double"
> typeof(23.5)
[1] "double"
> typeof(pi)
[1] "double"integer (ganze Zahlen)
Diese Ausgabe ist auf den ersten Blick verwirrend, da SchuelerIn_A die Zahl 13 zugewiesen wurde und somit ein integer sein müsste. Technisch speichert R die 13 als 13.0. Damit eine Zahl jedoch von R als ganze Zahl behandelt wird, muss hinter ihr ein L stehen:
> typeof(13L)
[1] "integer"
> SchuelerIn_X <- 9L
> typeof(SchuelerIn_X)
[1] "integer"Hinweis: Die Nachkommastellen einer Dezimalzahl wird immer durch einen Punkt . und nicht durch eine Komma , getrennt.
Character (Zeichenketten)
Character sind Zeichenketten (also meist Wörter), die in Anführungszeichen " " geschrieben werden müssen. Stehen Zeichenketten ohne Anführungszeichen in der R-Syntax, werden Zahlen als numeric und andere Zeichenketten als Objekte behandelt:
> SchuelerIn_Z <- "ausreichend"
> mode(SchuelerIn_Z)
[1] "character"
> mode(11)
[1] "numeric"
> mode("11")
[1] "character"
> mode(SchuelerIn_A)
[1] "numeric"
> mode("SchuelerIn_A")
[1] "character"Der Output der typeof() Funktion ist identisch zu dem der mode() Funktion.
> typeof(SchuelerIn_Z)
[1] "character"
> typeof(11)
[1] "double"
> typeof("11")
[1] "character"
> typeof(SchuelerIn_A)
[1] "double"
> typeof("SchuelerIn_A")
[1] "character"logical (logische Datentypen)
TRUE/FALSE (boolsche Variablen)
Die sogenannten booleschen Variablen (benannt nach dem Mathematiker George Boole) TRUE und FALSE sind das Ergebnis von logischen Vergleichsoperatoren (s.o.).
Boolesche Variablen können ebenfalls als Inhalte eines Objektes gespeichert werden. Z.B. speichern wir die Information, dass eine Lehrer*in ein naturwissenschaftliches Fach unterrichtet als TRUE und die gegenteilige Information als FALSE.
> LehrerIn_A <- TRUE
> LehrerIn_B <- FALSE
> LehrerIn_C <- TRUE
> LehrerIn_D <- FALSE
> LehrerIn_A == LehrerIn_C
[1] TRUE
> LehrerIn_A == LehrerIn_D
[1] FALSE
> LehrerIn_B < LehrerIn_A # TRUE ist immer größer als FALSE.
[1] TRUEDer Datentyp boolescher Variablen ist logical:
> mode(LehrerIn_A)
[1] "logical"
> typeof(LehrerIn_A)
[1] "logical"NA (Fehlende Werte)
Fehlende Werte sind in R ebenfalls ein Teil des Datentyps logical. Sie werden durch den Ausdruck NA ("not available") repräsentiert. Auch wenn die Ausprägung eines fehlenden Wertes unbekannt ist, kann sie dennoch der Inhalt eines Objektes sein.
> mode(NA)
[1] "logical"
> typeof(NA)
[1] "logical"Um dies zu verdeutlichen, stellen wir uns vor, dass neben den Notenpunkten der Schüler*innen A bis C (13, 11 und 10) auch die Notenpunkte einer vierten Schüler*in Y erhoben worden sind. Schüler*in Y hat zwar an der Evaluation teilgenommen, jedoch wurde für ihre Note kein gültiger Wert erhoben. Dies könnte mehrere Gründe haben:
-
Sie hat die Angabe verweigert.
-
Sie erinnerte sich nicht mehr an ihre Note.
-
etc.
In diesem Fall wird dem Objekt SchuelerIn_Y der Wert NA zugewiesen:
> SchuelerIn_Y <- NANun wollen wir die durchschnittliche Punktezahl der vier Schüler*innen (A, B, C und Y) ermitteln. Dafür werden alle Notenpunkte aufsummiert und durch die Anzahl der Schüler*innen dividiert:
> (SchuelerIn_A + SchuelerIn_B + SchuelerIn_C + SchuelerIn_Y) / 4
[1] NADa die Notenpunkte der Schüler*in Y unbekannt ist, könnten die Durchschnittsnotenpunkte eine beliebige Größe haben. Das Ergebnis der Rechnung ist also wiederum NA. (In diesem Beispiel könnten wir selbst eine Entscheidung darüber treffen, wie mit den Notenpunkten von Schüler*in Y umgegangen werden soll: Schließen wir sie aus der Berechnung aus?, Setzen wir für ihre Punktezahl einen konkreten Wert ein?, Rechnen wir mit einem Korrekturfaktor?...)
Um zu ermitteln, ob ein Objekt fehlende Werte beinhaltet, kann die Funktion is.na() genutzt werden:
> is.na(SchuelerIn_A)
[1] FALSE
> is.na(SchuelerIn_B)
[1] FALSE
> is.na(SchuelerIn_C)
[1] FALSE
> is.na(SchuelerIn_Y)
[1] TRUEViele Funktionen können mit einer Erweiterung definieren, wie mit fehlenden Werten umgegangen werden soll. Die Funktion min() berechnet den kleinsten Wert aus mehreren Argumenten. Wird der Erweiterung na.rm = der Wert TRUE zugeordnet, so werden fehlende Werte ignoriert:
> min(SchuelerIn_A, SchuelerIn_B, SchuelerIn_C, SchuelerIn_Y)
[1] NA
> min(SchuelerIn_A, SchuelerIn_B, SchuelerIn_C, SchuelerIn_Y, na.rm = TRUE)
[1] 10Vektoren (Sequenzen mit Datenelementen)
Vektoren in R sind Sequenzen, die Datenelemente umfassen. Es wird zwischen atomic vectors, lists und factors unterschieden.
atomic vector (Sequenzen mit gleichartigen Datenelementen)
Ein atomic vector ist eine Sequenz, die gleichartige Datenelemente umfasst — alle Elemente haben also denselben Datentyp (z.B. ausschließlich double oder ausschließlich character).
Wir könnten uns vorstellen, dass wir die Notenpunkte der Schüler*innen A bis C in einer gemeinsamen Gruppe (Gruppe_1) zusammenfassen. Diese Objekten bilden dann einen Vektor. In R erlaubt es die Funktion c() einen atomic vector zu erzeugen. Die einzelnen Vektorelemente müssen dabei durch Kommata separiert werden:
> Gruppe_1 <- c(SchuelerIn_A, SchuelerIn_B, SchuelerIn_C)
> Gruppe_1
[1] 13 11 10
> mode(Gruppe_1)
[1] "numeric"
> typeof(Gruppe_1)
[1] "double"Der Vektor Gruppe_1 umfasst nur Elemente mit dem Datentyp double, die Note der Schüler*in Z ist hingegen als character gespeichert worden. Wenn diese unterschiedlichen Datentypen in einem atomic vector zusammengefasst werden, speichert R alle Vektorelemente als gleichen Datentyp (in diesem Fall character):
> Gruppe_1_Z <- c(SchuelerIn_A, SchuelerIn_B, SchuelerIn_C, SchuelerIn_Z)
> Gruppe_1_Z
[1] "13" "11" "10" "ausreichend"
> mode(Gruppe_1_Z)
[1] "character"Jedes Vektorelement besitzt einen Index. Dieser beschreibt die Position des Elements im Vektor. SchuelerIn_B mit der Information 11 steht an der zweiten Position in dem Vektor Gruppe_1 und hat daher den Index 2. Der Index eines Vektorelements wird mit Vektorname[Index] angesprochen:
> Gruppe_1[2]
[1] 11Mit Vektoren können verschiedene Berechnungen vereinfacht werden:
> Gruppe_1 + 2 # Jedes Element eines Vektors wird mit einer Zahl addiert.
[1] 15 13 12
> Gruppe_1 / 3 # Jedes Element eines Vektors wird durch eine Zahl dividiert.
[1] 4.333333 3.666667 3.333333
> sum(Gruppe_1) # Die Funktion sum() erstellt die Summe von Objekten.
[1] 34
> SchuelerIn_A # Berechnungen mit einem Vektor verändern nicht die Objekte, die er umfasst.
[1] 13Die Datenstruktur eines Vektors kann mit der Funktion str() ausgegeben werden:
> str(Gruppe_1)
num [1:3] 13 11 10Ein Vektor kann mit der Funktion sort() sortiert werden — standardmäßig von der kleinsten zur größten Ausprägung:
> sort(Gruppe_1)
[1] 10 11 13
# Atomic vectors, die aus characters bestehen, werden alphabetisch sortiert (dabei sind Zahlen "kleiner" als Buchstaben):
> sort(Gruppe_1_Z)
[1] "10" "11" "13" "ausreichend"list (Sequenzen mit verschiedenartigen Datenelementen)
Im Gegensatz zu atomic vectors können lists auch Elemente mit verschiedenen Datentypen umfassen — also sowohl double und character, als auch andere wie atomic vectors, logicals, lists etc.
Lists werden in R mit der Funktion list() erzeugt. Auf diese Weise könnten wir eine Gruppe (Gruppe_2) mit den Schüler*innen A bis C und Schüler*in Z erstellen:
> Gruppe_2 <- list(SchuelerIn_A, SchuelerIn_B, SchuelerIn_C, SchuelerIn_Z)
> Gruppe_2
[[1]]
[1] 13
[[2]]
[1] 11
[[3]]
[1] 10
[[4]]
[1] "ausreichend"
> mode(Gruppe_2)
[1] "list"
> typeof(Gruppe_2)
[1] "list"
> str(Gruppe_2)
List of 4
$ : num 13
$ : num 11
$ : num 10
$ : chr "ausreichend"Wie atomic vectors besitzen lists einen Index mit dem die einzelnen Elemente angesprochen werden können:
> Gruppe_2[3]
[[1]]
[1] 10Allerdings kann mit lists nicht wie mit atomic vectors gerechnet werden:
> Gruppe_2 + 2
Error in Gruppe_2 + 2 : non-numeric argument to binary operator
> Gruppe_2 / 3
Error in Gruppe_2/3 : non-numeric argument to binary operator
> sum(Gruppe_2)
Error in sum(Gruppe_2) : invalid 'type' (list) of argument
> sort(Gruppe_2)
Error in sort.int(x, na.last = na.last, decreasing = decreasing, ...) :
'x' muss atomar seinfactor (gruppierte Vektoren)
Ein factor ist ein Vektor mit kategorialen Variablen. Das bedeutet, dass die Vektorelemente in eine logische Reihenfolge gebracht werden können. Ein Beispiel für eine kategoriale Variable sind die Monate eines Jahres; logischerweise beginnt ein Jahr im Januar und endet im Dezember.
Angenommen, wir kennen den Geburtsmonat von sechs verschiedenen Schüler*innen und speichern diese Information in einem atomic vector ("Geburtstage"):
SchuelerIn_D <- "Mai"
SchuelerIn_E <- "August"
SchuelerIn_F <- "Juli"
SchuelerIn_G <- "Mai"
SchuelerIn_H <- "September"
SchuelerIn_I <- "Februar"
Geburtstage <- c(SchuelerIn_D, SchuelerIn_E,
SchuelerIn_F, SchuelerIn_G,
SchuelerIn_G, SchuelerIn_I)
mode(Geburtstage)
[1] "character"Wird die sort() Funktion auf den Vektor angewendet, werden die Informationen der Vektorelemente alphabetisch sortiert:
> sort(Geburtstage)
[1] "August" "Februar" "Juli" "Mai" "Mai"
[6] "September"Die Monate ihrer Reihefolge im Jahr nach zu sortieren, funktioniert nicht mit einem atomic vector und der sort() Funktion. Um dies zu erreichen, muss ein factor erstellt werden ("Geburtstage_factor"). Ein factor besteht immer aus einem Vektor und dessen levels, also den sortierten möglichen Merkmalsausprägungen des Vektors. Der Vektor, der in diesem Beispiel verwendet wird, ist Geburtstage. Die levels des factors sind die Monate des Jahres. Diese werden ebenfalls als ein atomic vector in dem Objekt Monate gespeichert:
# Erstellung der levels des factors. Diese sind die Monate des Jahres.
Monate <- c(
"Januar", "Februar", "März",
"April", "Mai", "Juni",
"Juli", "August", "September",
"Oktober", "November", "Dezember"
)
# Erzeugen des factors. Der Vektor sind die Geburtstage der Schüler\*innen und seine levels die Monate des Jahres.
> Geburtstage_factor <- factor(Geburtstage, levels = Monate)
# Die Reihenfolge der Elemente des Vektors bleibt erhalten, jedoch kennt R nun ihre levels.
> Geburtstage_factor
[1] Mai August Juli Mai September Februar
12 Levels: Januar Februar März April Mai Juni Juli ... Dezember
# Die sort() Funktion kann die Monate in die korrekte Reihenfolge bringen.
> sort(Geburtstage_factor)
[1] Februar Mai Mai Juli August September
12 Levels: Januar Februar März April Mai Juni Juli ... Dezember
# Der Datentyp des factors ist "integer". Für R sind nicht die Namen der levels relevant, sondern ihr Rang:
# "Januar" = 1, "Februar" = 2, ... , "Dezember" = 12
> typeof(Geburtstage_factor)
[1] "integer"
# Dies wird besonders deutlich, wenn die Struktur des factors betrachtet wird.
# Er verfügt über 12 Levels. Das erste Element des factors (SchuelerIn_D) hat das level 5 (also "Mai"),
# das zweite Element (SchuelerIn_E) hat das level 8 ("August"), usw.
> str(Geburtstage_factor)
Factor w/ 12 levels "Januar","Februar",..: 5 8 7 5 9 2Index eines Vektors
Jedes Vektorelement hat eine Position innerhalb des Vektors — der sogenannte Index. Dieser kann genutzt werden, um auf bestimmte Elemente zuzugreifen. Ein Vektor steht immer in eckigen Klammer [] hinter den angeordneten Elementen:
> c(1,8,4,2)[2] # Gibt das zweite Element des Vektor wieder.
[1] 8
> c(1,8,4,2)[-2] # Hat als Ergebnis alle Vektorelemente außer dem zweiten.
[1] 1 4 2
> c(1,8,4,2)[c(1,3)] # Sollen mehrere Elemente eines Vektor angesprochen werden, müssen diese im Index selbst in einem Vektor stehen.
[1] 1 4
> c(1,8,4,2)[1:3] # Im Index kann auch eine Spanneweite stehen. Diese schließt sowohl deren Anfang (erstes Element) als auch ihr Ende (drittes Element) ein.
[1] 1 8 4Anhand der Beispiele können wir sehen, dass das erste Element eines Vektors immer den Index 1 hat. Das letzte Element eines Vektors entspricht immer der Länge des Vektors:
> length(c(1,8,4,2)) # Mit der length Function kann die Länge eines Vektors ermittelt werden.
[1] 4
> c(1,8,4,2)[length(c(1,8,4,2))] # Gibt das letzte Element des Vektor wieder. Dies ist besonders hilfreich bei Vektroren, die in einem Objekt gespeichert sind.
[1] 2
> c(1,8,4,2)[5] # Es gibt kein fünftes Element, daher kann ist das Ergebnis ein fehlender Wert.
[1] NA
> c(1,8,4,2)[0] # Ein Vektor hat kein "nulltes" Element. Daher ist das Ergebnis eine Zahl der Länge 0.
numeric(0)Als Beispiel wollen wir wissen, welche Notepunkte die zweite Schüler*in von Gruppe_1 bekommen hat:
> Gruppe_1[2]
[1] 11data.frame (Datensätze)
Aufbau
In einem Datensatz werden Informationen von mehreren Untersuchungseinheiten (z.B. Schulklassen) tabellarisch organisiert. Datensätze können in R als data.frames gespeichert werden.
Jede Spalte eines data.frame ist ein gleichlanger atomic vector, der die Ausprägungen eines Merkmals für alle Untersuchungseinheiten umfasst (z.B. die Anzahl der Schüler*innen von verschiedenen Schulklassen). Jede Zeile eines data.frame ist eine gleichlange list, in der die Ausprägungen aller Merkmale für eine Untersuchungseinheit stehen (z.B. alle Merkmalsausprägungen der Klasse 9a).
Als Beispiel wollen wir die folgende Tabelle als data.frame erzeugen, die Informationen von fünf Schulklassen (9a, 9b, 9c, 9d, 9e) enthält:
| Klasse | Anzahl_SchuelerInnen | KlassensprecherIn | Bilingual |
|---|---|---|---|
| 9a | 21 | SchuelerIn5 | Nein |
| 9b | 18 | SchuelerIn4 | Ja |
| 9c | 20 | SchuelerIn2 | Unbekannt |
| 9d | 21 | SchuelerIn3 | Nein |
| 9e | 28 | SchuelerIn1 | Ja |
Der data.frame besteht aus vier atomic vectors (Klasse, Anzahl_SchuelerInnen, KlassensprecherIn und Bilingual) und fünf lists (die Merkmalsausprägungen der jeweiligen Klasse):
# Die Elemente der Vektoren müssen in der korrekten Reihenfolge angeordnet sein.
Klasse <- c("9a", "9b", "9c", "9d", "9e")
Anzahl_SchuelerInnen <- c(21, 18, 20, 21, 28)
# Die Elemente des Vektors "KlassensprecherIn" sind characters!
KlassensprecherIn <- c("SchuelerIn5", "SchuelerIn4", "SchuelerIn2", "SchuelerIn3", "SchuelerIn1")
# Für das Merkmal "Bilingual" bietet es sich an, einen Vektor vom Datentyp logical zu erstellen.
Bilingual <- c(FALSE, TRUE, NA, FALSE, TRUE)Mit der Funktion data.frame() können atomic vectors zu einem einzigen Datensatz zusammengefasst werden (hier "Schulklassen").
Schulklassen <- data.frame(Klasse,
Anzahl_SchuelerInnen,
KlassensprecherIn,
Bilingual
)
> Schulklassen
Klasse Anzahl_SchuelerInnen KlassensprecherIn Bilingual
1 9a 21 SchuelerIn5 FALSE
2 9b 18 SchuelerIn4 TRUE
3 9c 20 SchuelerIn2 NA
4 9d 21 SchuelerIn3 FALSE
5 9e 28 SchuelerIn1 TRUEWie bei Vektoren kann die Struktur eines data.frame mit der Funktion str() betrachtet werden:
> str(Schulklassen)
'data.frame': 5 obs. of 4 variables:
$ Klasse : chr "9a" "9b" "9c" "9d" ...
$ Anzahl_SchuelerInnen: num 21 18 20 21 28
$ KlassensprecherIn : chr "SchuelerIn5" "SchuelerIn4" "SchuelerIn2" "SchuelerIn3" ...
$ Bilingual : logi FALSE TRUE NA FALSE TRUEUnserer Datensatz besteht aus fünf Beobachtungen (obs.) für jeweils vier verschiedene Variablen: zwei Variablen sind character (Klasse und KlassensprecherIn), eine ist numeric (Anzahl_SchuelerInnen) und eine logical (Bilingual).
Wie Vektoren, verfügen data.frames über einen Index. Dieser ist jedoch zweidimensional — es muss sowohl die Zeile als auch die Spalte angesprochen werden. Um dies zu gewährleisten, wird der Index [] durch ein Komma getrennt; [Zeilenindex,Spaltenindex]. Die erste Zahl im Index bezieht sich auf die Zeilen und die zweite auf die Spalten des data.frames:
# Wir wollen wissen, wie viele Schüler\*innen in Klasse 9c sind.
> Schulklassen[3, 2] # Die Daten der Klasse 9c befinden sich in der dritten Zeile. Die Anzahl der Schüler\*innen wird in der zweiten Spalte abgelesen.
[1] 20
# Es sollen nur die Daten der Klasse 9b ausgegeben werden.
> Schulklassen[2, ] # Die Daten der Klasse 9b befinden sich in der zweiten Zeile. Um alle Elemente einer Spalte auszuwählen, bleibt der Index leer.
Klasse Anzahl_SchuelerInnen KlassensprecherIn Bilingual
2 9b 18 SchuelerIn4 TRUE
# Es sollen die "Namen" der Klassensprecher\*innen von Klasse 9a und 9e ausgegeben werden.
> Schulklassen[c(1, 5), 3] # Um mehrere Elemente anzusprechen, werden diese in einem atomic vector geschrieben.
[1] "SchuelerIn5" "SchuelerIn1"Data.frames können auf zwei Wegen modifiziert werden — entweder ihre Zeilen werden verändert oder ihre Spalten.
Jede Zeile eines data.frame umfasst die Merkmalsausprägungen einer Beobachtung in Form einer list. Als Beispiel soll der vorhandene Datensatz durch die Daten von zwei Schulklassen ergänzt werden. Dafür wird die Funktion rbind() genutzt, in der der data.frame und die lists, um die dieser ergänzt werden soll, angegeben werden müssen:
Schulklassen_Neu <- rbind(Schulklassen,
list("10a", 16, "SchuelerIn7", FALSE),
list("10b", 22, "SchuelerIn6", FALSE))
> Schulklassen_Neu
Klasse Anzahl_SchuelerInnen KlassensprecherIn Bilingual
1 9a 21 SchuelerIn5 FALSE
2 9b 18 SchuelerIn4 TRUE
3 9c 20 SchuelerIn2 NA
4 9d 21 SchuelerIn3 FALSE
5 9e 28 SchuelerIn1 TRUE
6 10a 16 SchuelerIn7 FALSE
7 10b 22 SchuelerIn6 FALSEAchtung: In jeder list müssen Ausprägungen für alle Variablen angegeben werden:
# Hier fehlt die Ausprägung der Variable "Anzahl_SchuelerInnen".
> Schulklassen_Zeile_Fehler <- rbind(Schulklassen_Neu, list("10c", "SchuelerIn7", FALSE))
Error in xi[[j]] : subscript out of boundsWenn eine Zeile — und damit eine Beobachtung — gelöscht werden soll, muss diese mit einem negativen Vorzeichen im Index geschrieben werden:
# Löschen der dritten Zeile (Daten der Klasse 9c) des Datensatzes.
> Schulklassen_ohne_9c <- Schulklassen_Neu[-3, ]
> Schulklassen_ohne_9c
Klasse Anzahl_SchuelerInnen KlassensprecherIn Bilingual
1 9a 21 SchuelerIn5 FALSE
2 9b 18 SchuelerIn4 TRUE
4 9d 21 SchuelerIn3 FALSE
5 9e 28 SchuelerIn1 TRUE
6 10a 16 SchuelerIn7 FALSE
7 10b 22 SchuelerIn6 FALSEJede Spalte eines data.frame umfasst die Merkmalsausprägungen einer Beobachtung in Form eines atomic vectors. Als Beispiel soll der vorhandene Datensatz mit dem Schulfach der jeweiligen Klassenlehrer*in ergänzt werden. Um dies zu erreichen, wird die Funktion cbind() genutzt. In dieser muss der data.frame und die atomic vectors stehen. Dem atomic vector muss zusätzlich ein Name gegeben werden mit Name = :
Schulklassen_Faecher <- cbind(Schulklassen_Neu, Faecher = c(
"Mathe",
"Deutsch",
"Erdkunde",
"Chemie",
"Englisch",
"Mathe",
"Biologie"))
> Schulklassen_Faecher
Klasse Anzahl_SchuelerInnen KlassensprecherIn Bilingual Faecher
1 9a 21 SchuelerIn5 FALSE Mathe
2 9b 18 SchuelerIn4 TRUE Deutsch
3 9c 20 SchuelerIn2 NA Erdkunde
4 9d 21 SchuelerIn3 FALSE Chemie
5 9e 28 SchuelerIn1 TRUE Englisch
6 10a 16 SchuelerIn7 FALSE Mathe
7 10b 22 SchuelerIn6 FALSE BiologieAchtung: In jedem atomic vector müssen die Ausprägungen aller Untersuchungseinheiten angegeben werden:
# Hier werden nur sechs Ausprägung aufgelistet, obwohl unser Datensatz sieben Beobachtungen umfasst.
> Schulklassen_Spalte_Fehler <- cbind(Schulklassen_Neu, Durchschnittsnote = c(
1.8,
2.7,
1.9,
3.3,
2.0,
2.1))
Error in data.frame(..., check.names = FALSE) :
Argumente implizieren unterschiedliche Anzahl Zeilen: 7, 6Wenn eine Spalte gelöscht werden soll, muss diese mit einem negativen Vorzeichen im Index geschrieben werden:
# Löschen der vierte Spalte des Datensatzes (Information, ob die Klasse bilingual unterrichtet wird).
> Schulklassen_ohne_Bilingual <- Schulklassen_Faecher[, -4]
> Schulklassen_ohne_Bilingual
Klasse Anzahl_SchuelerInnen KlassensprecherIn Faecher
1 9a 21 SchuelerIn5 Mathe
2 9b 18 SchuelerIn4 Deutsch
3 9c 20 SchuelerIn2 Erdkunde
4 9d 21 SchuelerIn3 Chemie
5 9e 28 SchuelerIn1 Englisch
6 10a 16 SchuelerIn7 Mathe
7 10b 22 SchuelerIn6 BiologieWeitere
Packages
R bietet seinen Nutzer*innen die Möglichkeit Funktionen zu nutzen, die nicht standardmäßig in R enthalten sind. Diese zusätzlichen Funktionen sind in nutzer*innengeschrieben Paketen enthalten und können von den CRAN Mirrors heruntergeladen werden.
Installation
Als Beispiel wird das Paket tidyverse installiert, das mehrere Pakete zur Analyse von Datensätzen umfasst. Ein neues Paket wird mit der Funktion install.packages() installiert, dabei muss Paket als character (also mit Anführungszeichen) angesprochen werden:
>install.packages("tidyverse")
Installing package into ‘D:/R/win-library/4.0’
(as ‘lib’ is unspecified)
trying URL 'https://cran.rstudio.com/bin/windows/contrib/4.0/tidyverse_1.3.0.zip'
Content type 'application/zip' length 440077 bytes (429 KB)
downloaded 429 KB
package ‘tidyverse’ successfully unpacked and MD5 sums checked
The downloaded binary packages are in
C:\Users\AppData\Local\Temp\RtmpGiqR39\downloaded_packagesDas Paket ist nun erfolgreich auf dem eigenen Rechner installiert und seine integrierten Funktionen können in R verwendet werden. Um Funktionen eines Paketes nutzen zu können, muss dieses mit library() als Objekt geladen werden:
> library(tidyverse)
-- Attaching packages --------------------------------------- tidyverse 1.3.0 --
v ggplot2 3.3.2 v purrr 0.3.4
v tibble 3.0.3 v dplyr 1.0.2
v tidyr 1.1.2 v stringr 1.4.0
v readr 1.3.1 v forcats 0.5.0Hinweis: Pakete müssen bei jeder neuen R-Sitzung neu geladen werden (jedoch nicht installiert)!
Jetzt können Funktionen aus dem Paket tidyverse genutzt werden. Als Beispiel können nun mit drop_na() alle Zeilen eines Datensatzes gelöscht werden, in denen sich fehlende Werte befinden:
> drop_na(Schulklassen_Faecher, Bilingual)
Klasse Anzahl_SchuelerInnen KlassensprecherIn Bilingual Faecher
1 9a 21 SchuelerIn5 FALSE Mathe
2 9b 18 SchuelerIn4 TRUE Deutsch
3 9d 21 SchuelerIn3 FALSE Chemie
4 9e 28 SchuelerIn1 TRUE Englisch
5 10a 16 SchuelerIn7 FALSE Mathe
6 10b 22 SchuelerIn6 FALSE Biologie
# Der Wert der Klasse 9c für die Variable "Bilingual" war ein fehlender Wert, daher wurde die Zeile gelöscht.Hilfe
Egal ob Einsteiger*in oder jahrelanger Profi, es ist völlig normal bei der Arbeit mit R Fehlermeldungen zu produzieren oder bei manchen Anweisen nicht weiterzukommen. Da niemand alle R-Funktionen bzw. -packages kennen kann, ist es wichtig zu wissen, wie und wo Hilfe zu suchen ist.
Fehlermeldungen in R
Ungültige Anweisungen im Code erzeugen Fehler. Sobald der R-interpreter eine fehlerhafte Anweisung berechnet, wird ein Fehlermeldung in der R-Console angezeigt — der übrige Code wird dennoch ausgeführt.
> SchuelerIn_A + 1
[1] 14
> "Die erste Schüler_in hat die Note" + "sehr gut."
Error in "Die erste Schüler_in hat die Note" + "sehr gut." :
non-numeric argument for binary operator



